
Denna tvålfilm som finns i en metallstav har korsningar där flera tvålfilmer möter varandra. Under 2014, Professor Jenny Harrison från UC Berkley utökade lösningen på Plateau -problemet för att ta hänsyn till mer komplicerade tvålfilmsformer som den här. Upphovsman:Okinawa Institute of Science and Technology
Används ofta för barns roliga, tvålbubblor är känsliga, ljusreflekterande filmer som vanligtvis bara varar några sekunder innan de brister. Men bortom deras värde att underhålla, såpbubblor är fysiska exempel på det rika matematiska problemet med minimala ytor; de antar formen av minsta möjliga ytarea, som innehåller en given volym. Forskare vid Okinawa Institute of Science and Technology Graduate University (OIST) har nyligen utarbetat lösningen på ett matematiskt problem-känt som Kirchhoff-Plateau-problemet-som helt enkelt illustreras av tvålfilmer som spänner över flexibla slingor.
"Vår lösning på Kirchhoff -Plateau -problemet ger vackra matematiska resultat nära det som händer i den fysiska världen, "säger Dr Giulio Giusteri, medförfattare till tidningen som nyligen publicerades i Journal of Nonlinear Science. Dr Giusteri arbetade med professor Eliot Fried, som leder OIST:s Mathematical Soft Matter Unit, och doktor Luca Lussardi från Università Cattolica del Sacro Cuore i Italien.
Frågan som besvaras av teamet är en variant av "Plateau -problemet", ett hundraårigt matematiskt problem, uppkallad efter belgisk fysiker från 1800 -talet, Joseph Plateau. Plateau antog att när du doppar en stel trådram i en tvålösning, ytan på tvålfilmen som bildas på ramen representerar ett minimum matematiskt möjligt område, oavsett ramens form.
Den första tillfredsställande lösningen för platåproblemet gavs på 1900 -talet, av amerikansk matematiker Jesse Douglas, som han tilldelades Fields -medaljen 1936. På senare tid har under 2014, Professor Jenny Harrison från UC Berkeley förlängde Douglas arbete, tillhandahålla ett bevis som gäller under allmänna hypoteser som omfattar, till exempel, situationer där korsningar finns när flera tvålfilmer möter varandra.
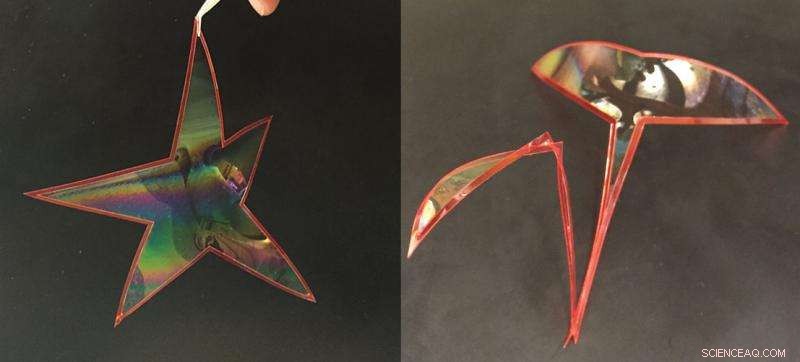
Tvålfilmer som finns i en flexibel slinga utövar en kraft på öglan, får den att ändra form. Till exempel, samma slinga kan bilda en stjärnform eller en svanform beroende på tvålfilmens ytspänning. Upphovsman:Okinawa Institute of Science and Technology
Till skillnad från Plateau -problemet där en tvålfilm sträcker sig över en fast ram, Kirchhoff-Plateau-problemet gäller jämviktsformer hos tvålfilmer som spänner över flexibla öglor, gjord, till exempel, av fiskelina, som kan beskrivas med Kirchhoffs teori om stavar - en modell som ger ett kraftfullt tillvägagångssätt för att studera statik och dynamik för tunna elastiska stavar. Komplikationen är att en flexibel slinga kan ändra form som svar på kraften som utövas av tvålfilmen. Som sådan, en lösning på problemet kräver att man inte bara bestämmer formen på tvålfilmen utan också formen på avgränsningsslingan. I kontrast, formen på gränsen i det ursprungliga platåproblemet är känd eftersom den är gjord av styv tråd som förblir fixerad mot tvålfilmens relativt svaga krafter.
En ytterligare komplikation i samband med Kirchhoff-platåproblemet är att till skillnad från det ursprungliga platåproblemet där gränsen antas vara endimensionell, en Kirchhoff-stav är ett tredimensionellt objekt. Även om filament som fiskelinje är tunna, de är storleksordningar tjockare än en tvålfilm i jämvikt, vilket innebär att tvålfilmens område kan förändras beroende på vid vilken punkt filmen kommer i kontakt med öglan.
Forskarna översatte framgångsrikt alla dessa fysiska effekter till matematiska termer. Som professor Fried förklarar:"Oavsett hur stark konkurrensen är mellan tvålfilmens ytspänning och slingans elastiska svar, systemet kan alltid justera för att uppnå en konfiguration med minst energi. "
Lösningen på Kirchhoff-Plateau-problemet bidrar inte bara till förståelsen av energi som minimerar matematiska former, men kan också appliceras på biologiska system. Till exempel, det kan hjälpa oss att förstå hur formen på ett protein avgör hur det interagerar med och binder till en yta.
Teamet arbetar nu med datasimuleringar som, baserat på denna matematiska modell, kan förutsäga beteendet hos fysiska system.