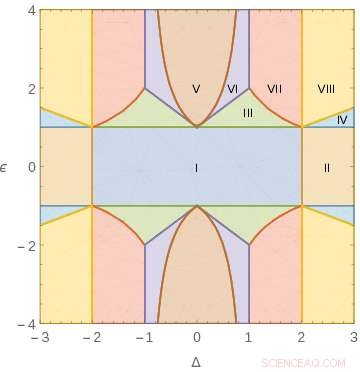
Parameterregioner med olika beteenden hos den klassiska gränsen för en XXZ-liknande Hamiltonian med två parametrar. Kredit:ICFO
Klassiska samband är en del av vår vardag. Till exempel, om man alltid tar på sig ett par strumpor av samma färg och form, tittar på färgen eller formen på en socka bestämmer färgen eller formen på dess par. Ännu mer, genom att observera färgen och formen på den ena strumpan och vi kan samtidigt känna till färgen och formen på den andra.
I kvantområdet, Heisenbergs osäkerhetsprincip säger att exakt mätning av ett par egenskaper hos en atom sätter en gräns för den mätnoggrannhet du kan få på samma egenskaper hos en annan atom. Därför, om strumporna sägs vara intrasslade, att observera färgen på den ena strumpan skulle tillåta oss att förutsäga färgen på den andra. Dock, om vi också observerar strumpans form, detta skulle "störa" färgen, vilket gör det helt oförutsägbart till viss del. Denna konstiga "synkronisering" mellan partiklar definieras som kvantinvikling, och är en av de inneboende egenskaperna i kvantvärlden.
I naturen, det finns en mycket främmande form av så kallade icke-lokala korrelationer, som manifesteras av vissa intrasslade tillstånd mellan atompartiklar. Genom att göra de minimala antaganden att egenskaper hos objekt (form/färg) existerar oavsett vår kunskap om dem, och att informationen inte kan spridas omedelbart, man finner att kvantfysiken kan generera korrelationer som är oförenliga med dessa två till synes rimliga principer.
Även om det är extremt fascinerande att studera, dessa icke -lokala korrelationer är mycket svåra att karakterisera i system som består av många partiklar av tre skäl. Först, klassiska korrelationer är matematiskt mycket komplexa att studera; andra, kvantkroppar med många kroppar är mycket komplexa att beskriva på grund av den exponentiella tillväxten av deras beskrivna tillstånd; och, tredje, för närvarande tillgängliga experimentella tekniker är ganska begränsade, begränsa de mätningar som kan utföras i laboratoriet. För att utforska rollen för icke-lokala korrelationer i kvantsystem i många kroppar, man måste alltså ta itu med dessa tre problem samtidigt.
I en ny tidning publicerad i Fysisk granskning X , ett team av forskare från MPQ i München, ICFO i Barcelona, Universitetet i Innsbruck och Centrum för teoretisk fysik vid polska vetenskapsakademien har föreslagit ett enkelt test för att studera icke-lokala korrelationer i kvantmångkroppssystem. De har studerat om icke -lokala korrelationer förekommer i naturliga system som grundtillstånd för några spinn Hamiltonians, till exempel elektroner (beskrivs av deras rotationsgrad av frihet) i ett system med en rumslig dimension. Genom att kombinera numeriska och analytiska resultat, de har visat att vissa Hamiltonianer som har studerats av fysiker i några decennier har ett tillstånd av minimal energi som kan visa icke -lokala korrelationer.
Som den första författaren, Jordi Tura, har kommenterat, "Vi tillhandahåller en uppsättning verktyg för att studera ett problem som alltid har varit komplicerat på egen hand. Teknikerna vi utvecklat är mycket enklare än tidigare. Om du ville implementera dem i labbet, du skulle bara behöva se till att systemet är förberett i ett tillstånd med tillräckligt låg energi. "
Resultaten belyser detta fascinerande problem, förhoppningsvis leda till ytterligare framsteg i vår förståelse av icke-lokalitet i kvantmångkroppssystem.