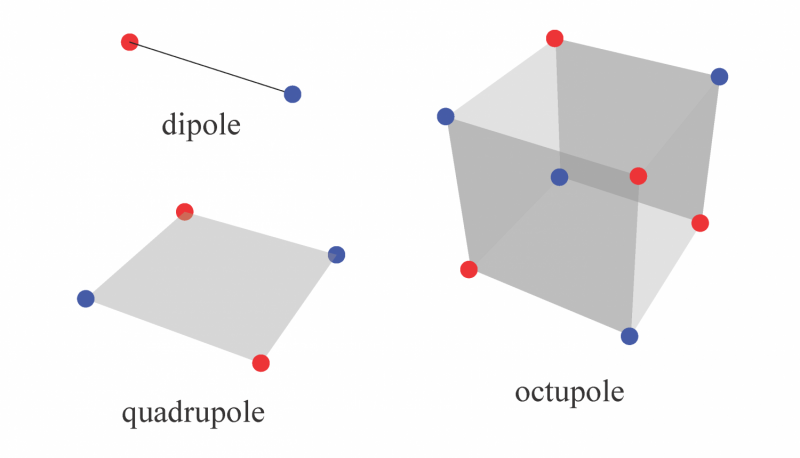
I denna figur, det elektriska dipolmomentet representeras av en positiv laddning (röd prick) och en negativ laddning (blå prick) som är rumsligt separerade. Fyrpolen, består av två motsatta dipolmoment, är i sig tvådimensionell, och oktupolen, består av två motsatta fyrdubbar, är i sig tredimensionell. Medan material med kvantiserade dipolmoment tidigare var kända, isoleringskristaller med kvantiserade kvadrupol- och oktupolmoment är topologiska faser till skillnad från alla som hittills hittats. Upphovsman:Wladimir Balcazar, Institutionen för fysik och institut för teori om kondenserad materia, University of Illinois i Urbana-Champaign.
Forskare vid University of Illinois i Urbana-Champaign och Princeton University har teoretiskt förutspått en ny klass av isolerande faser av materia i kristallina material, fastställt var de kan hittas i naturen, och i processen generaliserade den grundläggande kvantteorin för Berry -faser i solid state -system. Vad mer, dessa isolatorer genererar elektriska quadrupol- eller oktupolmoment - som ungefär kan betraktas som mycket specifika elektriska fält - som är kvantiserade. Kvantiserade observerbara är en guldstandard inom forskning om kondenserad materia, eftersom experimentella resultat som mäter dessa observerbara måste, i princip, matchar exakt teoretiska förutsägelser - lämnar inget utrymme för tvivel, även i mycket komplexa system.
Forskningen, vilket är den kombinerade insatsen av doktorand Wladimir Benalcazar och docent i fysik Taylor Hughes från Institute for Condensed Matter Theory vid U. och professor i fysik B. Andrei Bernevig från Princeton, publiceras den 7 juli, 2017 års nummer av tidningen Vetenskap .
Teamets arbete började med att identifiera en fyrpolig isolator, men det blev snart uppenbart att det fanns djupare konsekvenser.
Benalcazar förklarar, "En av de nya modellerna som verket presenterar har ett kvantiserat elektriskt fyrfaldigt ögonblick. Det är en isolator till skillnad från alla tidigare kända topologiska isolatorer. Den har inte gaplösa, lågenergiytor-kännetecknet för sådana system-vilket kan vara anledningen till att dessa system har undvikit upptäckt så länge. "
"Men anmärkningsvärt, " han fortsätter, "även om ytorna på fyrbandsisolatorn är gapade, de är inte obetydliga. Faktiskt, de bildar en lägre dimensionell topologisk isolatorfas! Våra beräkningar kan förutsäga när ett system kommer att rymma sådana topologiska isolatorer - vare sig det är på ytorna, gångjärn, eller hörn. Förvånande, denna egenskap i sin mest grundläggande form är relaterad till de högre elektriska multipolmomenten. "
Revolutionärt arbete under 1990- och 2000 -talen av Vanderbilt, King-Smith, Resta, Martin, Ortiz, Marzari, och Souza, gjort det möjligt att definiera dipolmomentet för en kristall genom en särskild tillämpning av Berry -fasen - en matematisk kvantitet som kännetecknar utvecklingen av elektronvågsfunktioner i gitterets momentum. Det arbetet representerade ett stort framsteg i vår förståelse av topologiska elektromagnetiska fenomen i kristallina material. Det gav en koppling mellan en fysisk kvantitet (dipolmoment) och en topologisk (bärfas). Enligt Hughes och Bernevig, den aktuella forskningen startade som ett försök att generalisera dipolmomentteorin till högre multipolmoment.
Hughes berättar, "I de tidigaste stadierna Andrei och jag diskuterade tanken på att utvidga arbetet med kristallina dipolmoment till fyrpoliga ögonblick. Men det visar sig, medan frågan verkade något självklar en gång, den matematiska lösningen var inte det. Att beräkna multipolmoment i ett kvantmekaniskt elektronsystem är utmanande eftersom elektronen, en kvantmekanisk partikel, är en våg, inte bara en partikel, och dess plats i rymden är osäker. Medan dipolmomentet kan nås genom att bara mäta elektronförskjutningen, en vektormängd, Fyrbandsstunderna är svårare. "
För att ta itu med detta, forskarna var tvungna att uppfinna en ny teoretisk ram. Dessutom, de behövde bygga modeller med rätt egenskaper genom vilka de kunde jämföra sin nya analytiska teknik. Men egentligen, saker hände i precis motsatt ordning:Hughes och Bernevig berömmer Benalcazar med att hitta rätt modell, en generalisering av en dipolisolator med ett kvantiserat dipolmoment. Därifrån, det tog ett helt år att bygga hela det teoretiska ramverket.
Befintliga matematiska verktyg-Berry-faserna i fast tillstånd-kunde bara lösa elektronens position i en riktning åt gången. Men för fyrbandsstunden, laget behövde bestämma sin position i två dimensioner samtidigt. Komplikationen härrör från
Heisenbergs osäkerhetsprincip, som vanligtvis säger att du inte kan mäta både position och momentum för en elektron samtidigt. Dock, i de nya fyrpoliga isolatorerna, en annan osäkerhetsprincip fungerar förhindra samtidig mätning av elektronens position i både X- och Y-riktningen. På grund av detta, författarna kunde inte rumsligt lösa elektronplatserna med hjälp av befintliga teoretiska verktyg.
"Vi kunde klämma fast det i en riktning, men inte den andra, "Benalcazar minns." För att få båda riktningarna samtidigt, vi skapade ett nytt analytiskt paradigm, i huvudsak genom att separera fyrpolsmomentet i ett par dipoler. "
Hughes tillägger, "I början, vi körde varje test vi visste hur vi skulle köra på de modeller vi föreslog och fortsatte att komma på ingenting. Problemet är, när två dipoler ligger ovanpå varandra, de avbryter varandra. För att se fyrpolen behöver du en rumslig upplösning för att avgöra om dipolerna faktiskt är separata. Till slut visade det sig, vi behövde titta på Berry -faserna ett lager djupare, matematiskt sett. "
Att hitta ett sätt att rumsligt lösa den andra dimensionen representerar ett betydande teoretiskt genombrott. Författarna utarbetade ett nytt paradigm för att beräkna platsen för elektroner som är en förlängning av Berry-fasformuleringen. Först, de använder en konventionell teknik för att teoretiskt dela upp elektronvågen i två laddningsmoln, separerade i rymden. Sedan visar de att varje moln har ett dipolmoment. Detta tvåsteg, kapslad procedur kan avslöja två rumsligt separerade, motsatta dipoler - en fyrdubbelpol.
Bernevig påpekar, "De topologiska isolatorer som vi har vant oss vid det senaste decenniet beskrivs alla i huvudsak av ett matematiskt förfarande som kallas att ta Berry -fasen i vissa elektroniska tillstånd. Berry -fasen i ett provs inre, i själva verket, vet om kanten på ett system - det kan berätta vad som är intressant med kanten.
För att gå ett steg bortom och lösa det som är potentiellt anmärkningsvärt i hörnet av ett system eller prov, du måste ta, i själva verket, en bärfas i en bärfas. Detta leder till formuleringen av en ny topologisk kvantitet som beskriver det kvantiserade kvadrupolmomentet. "
Under det senaste årtiondet, klassificeringen av topologiska faser av materia har utvecklats väsentligt. Betydande, detta nya verk visar fältets ännu outforskade rikedom. Den förutsäger en helt ny klass av faser och tillhandahåller modellen och teoretiska medel för att testa dess existens. Kanske en av de mest spännande aspekterna inom området topologiska isolatorer är deras experimentella relevans. I tidningsartikeln, laget föreslår tre möjliga experimentella inställningar för att validera deras förutsägelse.
Hughes erkänner att en kvantsimulering - en experimentell teknik som, till exempel, använder finstämda lasrar och ultrakylda atomer för att replikera och undersöka egenskaperna hos verkliga material - skulle vara det mest omedelbart tillgängliga.
"Det är spännande att använder nuvarande experimentell teknik, vår modell kan ses direkt, "Hughes bekräftar." Vi hoppas att vi eller någon annan så småningom hittar en elektronisk, solid-state material med denna typ av kvaliteter. Men det är utmanande, vi har ännu inte en kemisk formel. "
Författarna indikerar att förutsättningarna för att få denna effekt är ganska generella, och som sådan finns det många potentiella kandidater i många materialklasser.
"Eller insikten kan en dag komma från vänsterfältet, från någon annan helt genial implementeringsidé som någon kan tänka sig, "Bernevig kvittar.
Benzalcazar är övertygad om att "denna nya förståelse kan öppna en hel samling material som har denna hierarkiska klassificering."
Detta är grundforskning, och eventuella tillämpningar är fortfarande en avlägsen fråga om gissningar. Eftersom kvantiserade observationer möjliggör utsökt exakta mätningar, det är tänkbart att de nya elektriska egenskaperna hos denna nya materiefas kommer att vara användbara inom metrologi, elektronisk teknik, eller vid konstruktion av material med föreskrivna bulk/yta/kant/hörnegenskaper.
Författarna håller med, detta arbete öppnar många möjligheter för nya topologiska system som var dolda tidigare - dolda inom den inbyggda strukturen i Berry fas -matematiken. Dessa dolda topologiska faser har en skarp koppling till verkliga fysiska observationer - och det kan finnas andra fysiska fenomen i dessa material som skulle vara intressanta att utforska.