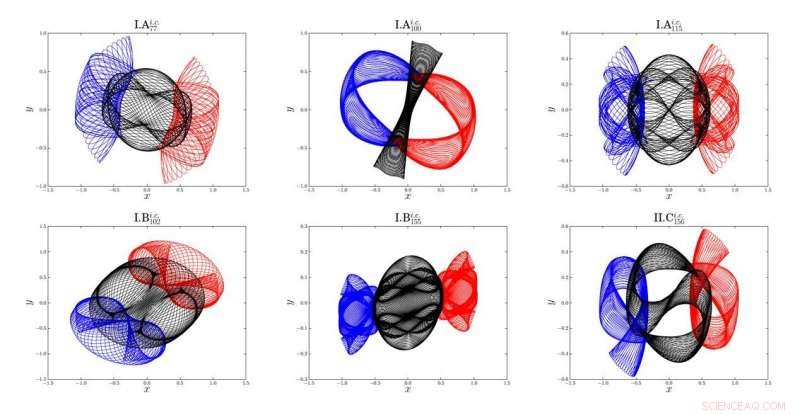
Kort översikt över de sex nyfunna familjerna i periodiska trekroppsbanor. Blå linje:bana av Body-1; röd linje:bana av Body-2; svart linje:bana av Body-3 Kredit:© Science China Press
Det berömda trekroppsproblemet kan spåras tillbaka till Isaac Newton på 1680-talet. Studier av trekroppsproblemet ledde till upptäckten av det så kallade sensitivitetsberoendet av initialtillstånd (SDIC) hos kaotiska dynamiska system. I dag, kaotisk dynamik betraktas allmänt som den tredje stora vetenskapliga revolutionen inom fysiken på 1900 -talet, jämförbar med relativitet och kvantmekanik. Således, studier om trekroppsproblemet har mycket viktig vetenskaplig betydelse.
År 1890, Poincare fastställde att banor för trekroppssystem vanligtvis är icke-periodiska, dvs inte upprepa. Detta kan förklara varför det är så svårt att få de periodiska banorna i trekroppssystem. Under de 300 år sedan trekroppsproblemet först erkändes, endast tre familjer av periodiska banor hade hittats. Under 2013, Suvakov och Dmitrasinovic [ Phys. Rev Lett. 110, 114301 (2013)] gjorde ett genombrott, hitta 13 nya distinkta periodiska banor som tillhör 11 nya familjer av det newtonska plana trekroppsproblemet med lika massa och noll vinkelmoment. Nu, två forskare, XiaoMing Li och ShiJun Liao vid Shanghai Jiaotong University, Kina, har framgångsrikt bestämt 695 familjer med periodiska banor i samma Newtonska plana trekroppssystem med hjälp av TH-2 superdator i Guangzhou, Kina. Deras resultat har publicerats i SCIENCE CHINA-Physics Mechanics &Astronomy . Videor av dessa banor finns här.
Dessa 695 periodiska banor inkluderar den välkända familjen åttasiffror som hittades av Moore 1993, de 11 familjer som Suvakov och Dmitrasinovic hittade 2013, och mer än 600 nya familjer rapporterade för första gången. De två forskarna använde den så kallade rena numeriska simuleringen (CNS), en ny numerisk strategi för tillförlitliga simuleringar av kaotiska dynamiska system som föreslogs av den andra författaren 2009, som är baserad på en stor ordning av Taylor -serier och flera precisionsdata, plus en konvergens/tillförlitlighetskontroll. CNS kan minska trunkeringsfel och avrundningsfel så effektivt att numeriskt brus är försumbart under tillräckligt lång tid, sålunda kan fler periodiska banor i trekroppssystemet erhållas.
Som rapporterades av Montgomery 1998, varje periodisk bana i det verkliga rummet i trekroppssystemet motsvarar en sluten kurva på den så kallade "formkulan, " som kännetecknas av sin topologi genom att använda det så kallade "fria gruppelementet." Medelperioden för en omloppsbana är lika med omloppsperioden dividerad med längden av motsvarande fria gruppelement. Dessa 695 familjer föreslår att kvadraten av den genomsnittliga perioden gånger kuben för den totala kinetiska och potentiella energin är ungefär lika med en konstant. Den generaliserade Keplers tredje lag avslöjar att trekroppssystemet har något gemensamt som kan fördjupa förståelsen av trekroppssystem.
Enligt forskarna, upptäckten av de mer än 600 nya periodiska banorna beror främst på framstegen inom datavetenskap och användningen av den nya strategin för numerisk simulering för kaotiska dynamiska system, nämligen CNS. Det bör understrykas att 243 fler periodiska banor i trekroppssystemet hittas med hjälp av CNS. Med andra ord, om traditionella algoritmer med dubbel precision användes, cirka 40 procent av de nya periodiska banorna skulle gå förlorade. Detta indikerar nyheten och originaliteten i CNS, eftersom alla nya metoder måste erbjuda något nytt.