Quantum computing ligger vid tröskeln för att ta itu med viktiga problem som inte kan beräknas effektivt eller praktiskt av andra, mer klassiska medel. Att komma förbi denna tröskel kommer att kräva att vi bygger, testa och använda tillförlitliga kvantdatorer med 50 eller fler qubits.

För att uppnå denna potential krävs stora framsteg inom både vetenskap och teknik. För att hjälpa till med att göra dessa språng, metoder behövs för att testa kvantanordningar och för att jämföra observerade beteenden med önskat beteende så att designen, tillverkning, och driften av dessa enheter kan förbättras med tiden. Särskilt, för att testa om de uppmätta resultaten som observerats på en kvantanordning överensstämmer med den kvantkrets som utförs, man behöver förmågan att beräkna förväntade kvantamplituder (komplexa tal som används för att beskriva systemets beteende) för dessa resultat för att testa godtyckliga kretsar. Kvantkretsar kan ses som uppsättningar instruktioner (grindar) som skickas till kvantanordningar för att utföra beräkningar.

Det behovet ställde oss inför ett problem. Vid ungefär 50 qubits, befintliga metoder för att beräkna kvantamplituder kräver antingen för mycket beräkning för att vara praktiskt, eller mer minne än vad som är tillgängligt på någon befintlig superdator, eller båda. IBM Research sammanställde ett team i år för att studera detta problem, inriktning på kortdjupskretsar för system på 49 qubits och längre. Vi har publicerat vårt tillvägagångssätt för att lösa detta problem till arXiv:arxiv.org/abs/1710.05867.

Jag var en del av detta team och kom på en nyckelidé vid ett till synes obetydligt ögonblick.

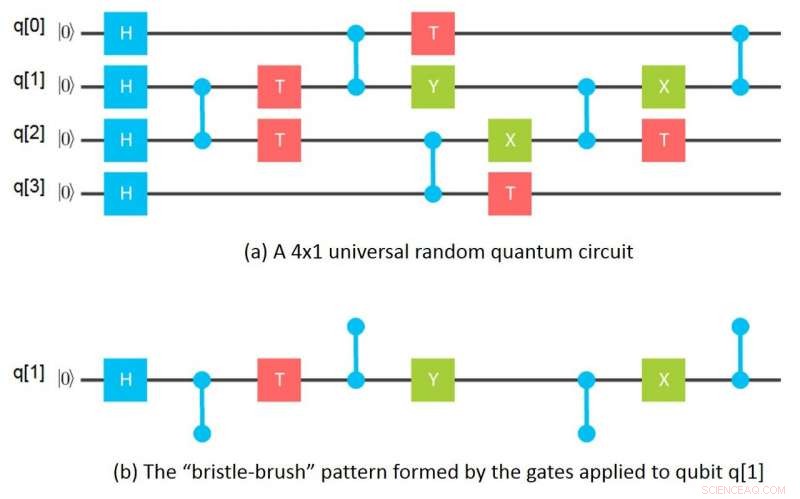
Visualisera kvantportar som borste

En qubit, eller kvantbit, är den grundläggande informationsenheten i kvantberäkning, precis som lite är i klassisk databehandling. En qubit, dock, kan representera både 0 och 1 samtidigt - faktiskt i viktade kombinationer (t.ex. 37%-0, 63%-1). Två qubits kan representera fyra värden samtidigt:00, 01, 10, och 11, igen i viktade kombinationer. Liknande, tre qubits kan representera 2^3, eller åtta värden samtidigt:000, 001, 010, 011, 100, 101, 110, 111. Femtio qubits kan representera över en kvadrillionsvärden samtidigt, och 100 qubits över en kvadrillion i kvadrat.

När qubits mäts, deras kvanttillstånd kollapsar till endast ett av dessa representerade värden, där värdenas vikter - kvantamplituderna - definierar sannolikheten för att observera dessa värden. Det stora löftet om kvantberäkning är potentialen att utföra parallella beräkningar över exponentiellt många möjliga resultat, att ge kvanttillstånd där de önskade resultaten av beräkningar har stora amplituder och, därav, kommer att observeras med stor sannolikhet när qubits mäts.

Mitt till synes obetydliga ögonblick kom en natt när jag diskade och använde en borste för att rengöra ett högt glas. Det kom plötsligt för mig att om man tittar på portarna som appliceras på en given qubit i en nätkrets, grindarna bildar ett borstborstmönster där borsten är de intrasslade grindarna som appliceras på den qubit. Matematiskt, att "borstborste" av grindar motsvarar en tensor och borsten för tensorindex. En tensor i matematik motsvarar i huvudsak en n-dimensionell matris inom datavetenskap.

Denna insikt ledde omedelbart till tanken att dra isär en nätkrets i enskilda "borstborstar, "en för varje qubit, sedan beräkna motsvarande tensorer, och slutligen kombinera tensorerna för varje qubit för att beräkna kvantamplituderna för den totala kretsen. Nästa morgon hade jag kommit på hur man beräknade amplituder för en 64 -qubit, djup 10 krets med endast en gigabyte minne genom att dra grupper på 16 qubits isär. Därifrån snöade idén till mer generella sätt att dela upp kretsar i underkretsar, simulera delkretsar separat och kombinera resultaten av underkretsar i olika ordningar för att beräkna önskade amplituder.

Nettoresultatet är en metod för att beräkna kvantamplituder som kräver storleksordningar mindre minne än tidigare metoder samtidigt som de är jämförbara med de bästa av dessa metoder, när det gäller mängden beräkning per amplitud. Dessa mindre minneskrav uppnås med tensorsnittning i kombination med insikterna som nämns ovan för att beräkna utmatningsamplituder för kretsar i skivor, utan att behöva beräkna och/eller lagra alla amplituder samtidigt.

Vid beräkning av amplituder för uppmätta utfall, bara de skivor som motsvarar de faktiska uppmätta resultaten behöver beräknas. Med andra ord, för att utvärdera prestanda för en kvantanordning baserat på uppmätta resultat, en fullständig simulering är inte nödvändig och man behöver inte ådra sig beräkningskostnader som är exponentiella i antalet qubits. Detta är en viktig fördel med vårt tillvägagångssätt.

Dock, om man faktiskt är intresserad av att utföra fullständiga simuleringar, vår skivningsmetod har en ytterligare fördel genom att skivor kan beräknas helt oberoende på ett pinsamt parallellt sätt-vilket innebär att de enkelt kan separeras-vilket gör att beräkningar kan distribueras över ett nätverk av löst kopplade högpresterande datorresurser. Denna möjlighet förändrar helt ekonomin i fullständiga simuleringar, möjliggör simulering av kvantkretsar som man tidigare trodde var omöjliga att simulera.

Simulerar 49 och 56 qubit kretsar med en superdator

Vårt forskargrupp kontaktade Lawrence Livermore National Laboratory (LLNL) och University of Illinois för att förverkliga den senare möjligheten. Med hjälp av Vulcan superdator på LLNL och Cyclops Tensor Framework som ursprungligen utvecklades vid University of California, Berkeley för att göra tensormanipulationerna, vi valde först att simulera en 49 -qubit universell slumpmässig krets med djup 27, som har föreslagits som en demonstration av så kallad kvantöverlägsenhet. För denna simulering, beräkningarna delades upp i 2^11 skivor med 2^38 amplituder beräknade per skiva; 4,5 Terabyte krävdes för att hålla tensorvärdena. Skivberäkningar var pinsamt parallelliserade över sex grupper om fyra rack med processorer, där varje grupp med fyra ställningar omfattade 4, 096 bearbetningsnoder med totalt 64 Terabyte minne. Sådana 49-qubit kretsar ansågs tidigare vara omöjliga att simulera eftersom tidigare metoder skulle ha krävt åtta petabyte minne, som överskrider kapaciteten hos befintliga superdatorer.

För vår nästa demonstration, vi valde en 56 -qubit universell slumpmässig krets med djup 23, vilket skulle ha varit omöjligt att simulera med tidigare metoder eftersom en Exabyte minne skulle ha krävts. Beräkningarna delades in i 2^19 skivor med 2^37 amplituder vardera. Men i detta fall valde vi att beräkna amplituder för endast en godtyckligt vald skiva för demonstrationsändamål; 3,0 Terabyte krävdes för att hålla tensorvärden och beräkningar utfördes på två rack med 2, 048 bearbetningsnoder med totalt 32 Terabyte minne.

Förutom dessa demonstrationer, vi upptäckte också sätt att dela upp 49-qubit kretsen så att endast 96 gigabyte minne behövs för dess simulering, med bara något mer än det dubbla av beräkningskraven. Vi upptäckte också en partitionering som kräver 162 gigabyte för vilka det knappt finns någon ökning av beräkningskraven. Möjligheten finns därför att nu utföra dessa simuleringar på kluster av avancerade servrar, istället för att använda superdatorer.

Framsteg inom simulering kommer att hjälpa framsteg inom kvantmaskinvara

Även om hela omfattningen av vad som nu är klassiskt beräknad med våra metoder fortfarande återstår att bestämma, det är klart att detta framsteg har gjort det möjligt för oss att passera ett tröskelvärde i simuleringen av kvantkretsar med korta djup på 49 qubits och större. Pragmatiskt, metoderna kommer att underlätta testning och förståelse för hur fysiska enheter fungerar. De kommer också att underlätta utvecklingen och felsökningen av kortdjupade algoritmer för problem där kvantberäkning har potential att ge verkliga fördelar jämfört med konventionella metoder.

Åtminstone för kvantanordningar som nu är under utveckling eller på ritbrädorna, förmågan att utföra dessa simuleringar har nu blivit en fråga om mängden beräkningsresurs som ekonomiskt kan anskaffas och inte om simuleringarna alls kan utföras fysiskt. Till exempel, i fallet med vår 56-qubit simulering, en fullständig simulering utfördes inte bara för att vår tidsfördelning på Vulcan hade tagit slut. Det är ingen tvekan om att en fullständig 56-qubit kortdjupssimulering nu kan utföras fysiskt. Körtiderna för dessa simuleringar begränsas inte heller fysiskt av de resurser som finns tillgängliga på isolerade datorsystem. Eftersom skivberäkningar kan vara pinsamt parallella, de kan distribueras över nätverk av löst kopplade system med minimal kommunikation, tillåter stark skalbarhet upp till antalet skivor. Molnbaserad kvantsimulering kan i slutändan tillåta att ganska stora kvantkretsar simuleras.

Innebär detta att vi inte behöver faktiska kvantdatorer? Inte alls. Vi kommer absolut att behöva dem! Beroende på vilken typ av applikation, vi kommer att behöva fysiska kvantdatorer för att utföra beräkningar som antingen kommer att kräva för mycket minne, eller för mycket processorkraft för att kunna utföras ekonomiskt på klassiska datorer. Och, vid något tillfälle, vi kommer verkligen att ha bevis för att kvantdatorer kommer att ha en fördel jämfört med klassiska datorer för några praktiska tillämpningar, i en verklig mening.

Detta är inte någon konstgjord uppfattning om "kvantöverlägsenhet". Snarare, vi befinner oss nu i en period där vi gör oss kvantklara för att dra full nytta av kvanthårdvaran, programvara och tekniska funktioner som vi lägger online. Simulering är redan en integrerad del av denna kvantfärdiga fas.

IBM har gjort tillgång till simulatorer och verklig hårdvara på fem och 16 qubits tillgängliga som en del av IBM Q -upplevelsen, som ger resurser att lära sig och experimentera med. Vi har också ett kvant -SDK, eller Quantis Information Software Kit (QISKit) för att göra det enkelt att bygga kretsar. För att lära dig mer om hur du kommer igång, vi har tillhandahållit Jupyter notebook -exempel på github.

När enhetstekniken utvecklas, vi kommer att gå in i en period med kvantfördel där ett brett spektrum av företag, forskare och ingenjörer kommer att utnyttja hårdvaran och kraften i kvantberäkningen fullt ut för att fortsätta lösa allt svårare och mer komplexa problem. Under denna kvantfördelningsfas, avancerade simuleringsmöjligheter kommer att behövas för att stödja både forskning och utveckling av nya kvantalgoritmer samt utvecklingen av själva tekniktekniken.