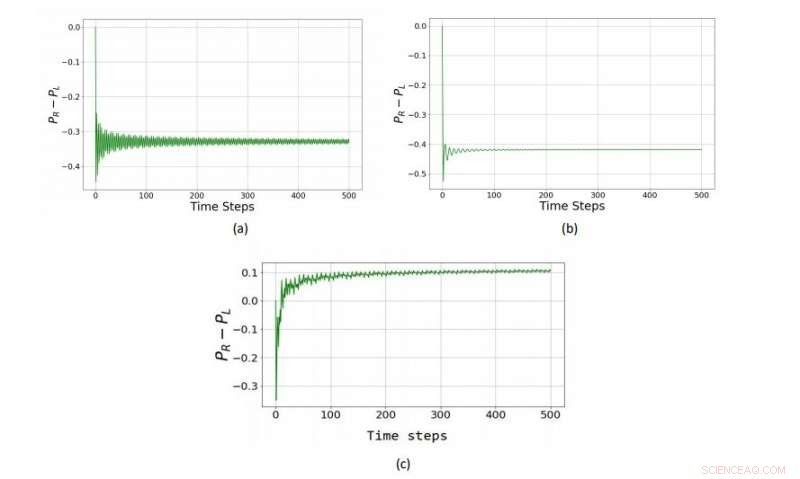
I en kvantversion av ett Parrondos spel spelat med ett trestatsmynt (en qutrit), de två förlorande strategierna (a) och (b) kombineras till en vinnande strategi (c). Upphovsman:Rajendran et al. © 2018 EPL
Fysiker har visat att Parrondos paradox - en uppenbar paradox där två förlorande strategier kombineras för att skapa en vinnande strategi - kan framstå som ett myntspel med ett enda mynt i kvantområdet, men bara när myntet har tre tillstånd (huvuden, svansar, och en sida) snarare än de konventionella två.
I allmänhet, Parrondos paradox, kallas också ett Parrondos spel, fungerar bara när de två förlorande strategierna på något sätt är beroende av varandra och kombineras på ett sådant sätt att de villkor som leder till att de förlorar ändras. Ända sedan det upptäcktes av fysikern Juan Parrondo 1996, Parrondos paradox har hittat tillämpningar inom teknik, finansiera, och evolutionär biologi, bland andra områden.
Ett av de enklaste sätten att implementera ett Parrondos spel beskrivs i denna Wikipedia -post. Antag att du har $ 100, och du kan välja att spela vilken kombination som helst av två spel. I det första spelet, du förlorar $ 1 varje gång du spelar. I det andra spelet, du vinner $ 3 om du har ett jämnt antal dollar kvar, och du förlorar $ 5 om du har ett udda antal dollar kvar. Om du bara spelar det första spelet eller bara spelar det andra spelet, du kommer så småningom att förlora alla dina pengar, så att spela varje spel i sig är en förlorande strategi. Dock, om du växlar mellan de två spelen, börjar med det andra spelet, då vinner du $ 2 för vartannat spel du spelar, så de två förlorande strategierna kan kombineras till en vinnande strategi.
I den nya studien, fysikerna Jishnu Rajendran och Colin Benjamin vid National Institute of Science Education and Research, HBNI, i Indien, har demonstrerat ett Parrondos spel med ett trestatsmynt, som de representerar med en qutrit, ett kvantsystem med tre tillstånd.
"Parrondos spel har setts i ett klassiskt sammanhang, "Berättade Benjamin Phys.org . "Vårt mål med detta arbete var att visa hur man implementerar det i ett kvantkontext, i synnerhet i en kvantpromenad. Tyvärr, kvantversionen av detta spel när det implementerades med ett enda mynt (qubit) i en kvantpromenad misslyckades i de asymptotiska gränserna. Det vi visar i detta arbete är att en qutrit kan implementera detta Parrondos spel i en kvantpromenad. "
I kvantpromenaden, en spelare börjar vid ursprunget och rör sig antingen höger (positiv riktning) eller vänster (negativ riktning) beroende på resultatet av ett myntkast. Om huvuden, spelaren rör sig åt höger; om svansar, vänster; och om resultatet är "sida, "då tolkar spelaren det som ett" väntetillstånd "och stannar på samma plats. Eftersom qutrit är ett kvantsystem, det kan också vara i en superposition av dessa tillstånd, i så fall flyttar spelaren till en motsvarande position, någonstans mellan ett helt steg till vänster eller höger. I slutet av spelet, om sannolikheten för att spelaren finns till höger om ursprunget är större än sannolikheten att hittas till vänster om ursprunget, spelaren vinner. Annat, de förlorar.
Med hjälp av några av standardmetoderna inom partikelfysik för att definiera begreppen myntkastning och spelregler med en överlagring av tillstånd, fysikerna visade flera exempel på spel som resulterar i förlust när de spelas individuellt, men när de kombineras i en växlande sekvens resulterar det i ett vinnande resultat. De demonstrerade också exempel på det omvända. Till exempel, två matcher som resulterar i vinst och oavgjort när de spelas individuellt kan resultera i ett förlorande resultat när de kombineras.
Fysikerna visade också att även om det inte är möjligt att implementera ett Parrondos spel med ett enda dubbelsidigt mynt (qubit), det är möjligt att implementera ett Parrondos spel med två dubbelsidiga mynt (två qubits). De ytterligare staterna ger i huvudsak ytterligare flexibilitet för att kombinera strategier som kan övervinna villkoren för att förlora.
Med tanke på de breda tillämpningarna av klassiska Parrondos spel, fysikerna förväntar sig att kvantversionen kan leda till ny insikt i utformningen av kvantalgoritmer.
"Parrondos spel är ett recept för att bevisa att man inte alltid behöver leta efter en vinnande strategi (eller algoritm) i ett spel, "Sade Benjamin." Klassiskt sett, det finns många tillämpningar av Parrondos spel, allt från att förklara fysiologiska processer i cellen till att öka vår förståelse för bruna motorer och till och med i diversifierade portföljinvesteringar. Klassiskt, Parrondos paradox har visat sig fungera med klassiska slumpmässiga promenader.
"Att implementera ett Parrondos spel i en kvantpromenad skulle få konsekvenser för att utforma bättre eller snabbare kvantalgoritmer. En algoritm som använder kvantprinciper som superposition och/eller intrassling är en kvantalgoritm. En algoritm, om det kan implementeras på en kvantpromenad, skulle vara mer lukrativ än en som bara kan implementeras på en klassisk slumpmässig promenad. När kvantpromenader sprider sig kvadratiskt snabbare än klassiska slumpmässiga promenader, en algoritm implementerad på en kvantgång tar mycket kortare tid att genomföra än en på en klassisk slumpmässig promenad. Ytterligare, den framgångsrika implementeringen av Parrondos spel på en kvantpromenad ger en algoritmisk förklaring till kvantspärrar [system som bara har rörelse i en riktning]. "
© 2018 Phys.org