
Matematiken för regndroppar. Upphovsman:Stefan Holm/shutterstock.com
Har du någonsin tagit en promenad genom regnet på en varm vårdag och sett den perfekta pölen? Du vet, den där regndropparna verkar röra sig i lagom takt, orsakar en dans av försvinnande cirklar?
Redan innan jag kom in på vätskeflödesforskning för nästan 15 år sedan, Jag fascinerades av vågorna som dyker upp efter att en regndroppe träffar en pöl.
När jag fokuserade på att studera instabila vågor i flytande ark - inriktade på att mildra oönskade vågor i industriella beläggnings- och atomiseringsprocesser - blev min fascination för pölvågor till en besatthet. Vad händer? Var kommer mönstret ifrån? Varför ser effekten av regn i en pöl annorlunda ut än när regn faller någon annanstans, som i en sjö eller havet?
Det visar sig att allt har att göra med något som kallas dispersion.
I samband med vattenvågor, dispersion är förmågan hos vågor med olika våglängder att var och en röra sig med sina egna individuella hastigheter. Ser ner på en pöl, vi ser en samling av sådana vågor som rör sig tillsammans som en krusning i vattnet.
När en regndroppe kommer ner, tänk dig det som en "ding" till vattenytan. Denna ding kan idealiseras som ett paket med vågor i alla olika storlekar. Efter att regndroppen faller, paketets vågor är redo att börja sitt nya liv i pölen.
Dock, om vi ser dessa vågor som krusningar beror på den vattensamling som regndroppen landar på. Antalet och avståndet mellan ringarna som du ser beror på vattenpölens höjd. Detta har verifierats i några väldigt coola rippeltanksexperiment, där en droppe med samma hastighet faller i en behållare med vatten på olika djup.
Korta pölar möjliggör krusningar, eftersom de är mycket tunnare än de är breda. Balansen mellan ytkraften - mellan vattenpölen och luften ovanför den - och gravitationskraften spetsar till förmån för ytkraft. Det här är nyckeln, eftersom ytkraften beror på krökningen hos vattenytan, medan gravitationskraften inte gör det.
En från början fortfarande ytlig pöl blir krökt vid ytan efter att regndroppen träffat. Ytkraften är annorlunda för långa vågor än för korta, vilket gör att vågor av olika storlekar separeras i krusningar. För grunda vattenpölar, de långa vågorna rör sig långsamt bort från stötpunkten, medan de korta vågorna rör sig snabbt, och de riktigt korta vågorna rör sig riktigt snabbt, blir tätt packade i omkretsen. Detta skapar det förtrollande mönstret som vi ser.
Regndroppar kan reagera annorlunda i andra situationer. Tänk dig att regnet slår mot en sjö eller ett hav - eller de djupa gropar som kräver galoscher. Här, regndroppen träffar vattnet, men kraften på grund av gravitationen blir viktigare. Den förflyttar vågor av alla storlekar med samma hastighet som kan överväldiga den krusande effekten på grund av ytkraften.
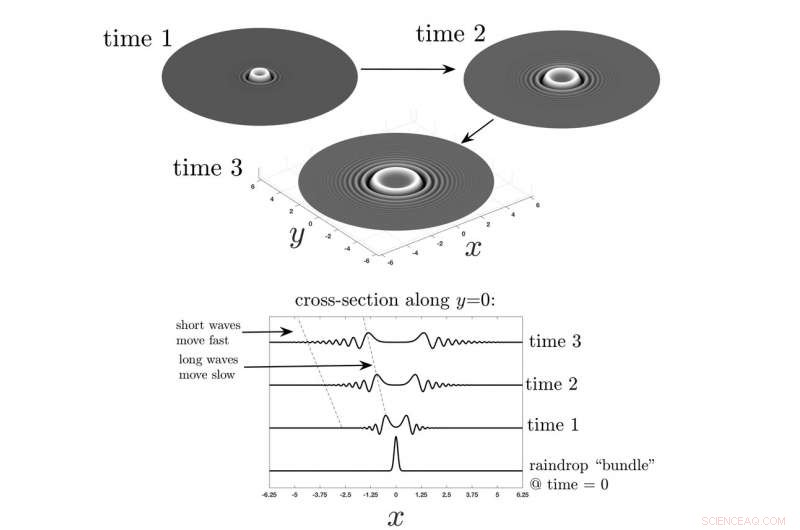
En modell av vågor i en spridande pöl, efter att en regndroppe träffat. De tre bästa siffrorna visar vad som händer efter att en droppe träffar pölen, med pilar som indikerar tidens gång. Den nedre figuren visar tvärsnittsvy genom pölen, betonar att det första vågpaketet som orsakas av regndroppen delar sig i vågor av olika storlekar. Stora vågor i mitten rör sig långsammare än små vågor vid omkretsen. Upphovsman:Nate Barlow
Kombinationen av att undervisa i grunddifferentiella ekvationer samtidigt som man fortsatte att undersöka vätskeark ledde till vad jag har kallat "pölekvationen". När det är löst, ekvationen skapar en animerad simulering av vad som händer efter att en regndroppe träffar en pöl. Det är en förenklad version av en ekvation i en av vår grupps nyare forskningsinsatser, men det överensstämmer också med den klassiska beskrivningen av krusningar.
Jag använder den här ungefärliga beskrivningen av pölvågor som ett sätt att få eleverna upphetsade över matematik genom att relatera den till omvärlden.
Studiet av ytkraftdrivna vågor är viktigt för applikationer som beläggningsprocesser som är involverade i tillverkning av batterier och solceller.
Sådana vågor uppträder också som ett resultat av bensträckan hos en vattenstriderinsekt, men forskning har funnit att vattenstridaren inte specifikt vill göra dessa vågor för att möjliggöra resor.
Skönheten i pölvågor är ingen liten sak i sig. Genom att ansluta naturen med sitt urspråk - matematik - får vi tillgång till dess kontrollpanel, tillåter oss att observera varje liten detalj, avslöjar alla hemligheter.
Denna artikel publiceras från The Conversation under en Creative Commons -licens. Läs originalartikeln. 