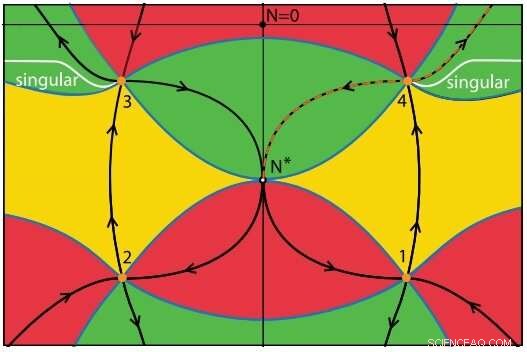
Den orange streckade linjen visar att sökvägsintegralen, som beskriver universums tillstånd över tid, passerar endast en sadelpunkt, som är stabil. Kredit:Di Tucci och Lehners. © 2019 American Physical Society
En idé för hur universum började är att universum kan ha dykt upp ur ingenting på grund av någon kvanteffekt, som kvanttunnel. På 1980 -talet, Stephen Hawking och James Hartle utarbetade vidare denna idé genom att föreslå att tiden inte fanns före universums början, får dem att dra slutsatsen att universum inte har några initiala gränsvillkor för varken tid eller rum. Idén kallas "förslaget utan gräns" eller "Hawking-Hartle-staten".
Dock, att exakt beskriva hur ett fysiskt system kan övergå från nollstorlek till en ändlig storlek har varit utmanande. För att beskriva de involverade kvanteffekterna, fysiker använder vägen integrerad formulering, som innebär omskrivning av en enda klassisk bana som en integral över många möjliga banor, vilket resulterar i en kvantamplitud.
Även om vägintegralformuleringen är framgångsrik i att beskriva hur något kan komma ur ingenting, ett stort problem är att det förutspår instabila störningar, vilket innebär att universum är mycket icke-homogent och icke-isotropiskt. Eftersom universum är känt för att vara ungefär både homogent och isotropiskt (vilket betyder att det ser likadant ut på alla platser och från alla håll), enligt den kosmologiska principen, vägintegralformuleringen beskriver inte det observerade universum exakt. Detta har fått vissa forskare att dra slutsatsen att förslaget utan gränser inte kan ge en korrekt beskrivning av universums ursprung.
Nu i ett nytt papper, fysiker Alice Di Tucci och Jean-Luc Lehners vid Max Planck Institute for Gravitational Physics (Albert Einstein Institute) i Potsdam, Tyskland, har visat att vägintegralformuleringen kan användas på ett sätt som undviker instabilitet, samtidigt som den ger en konsekvent definition av förslaget om gränslöshet.
"Jag tror att den största betydelsen är att vår nya definition inte beskriver universums uppkomst från en fullständig frånvaro av utrymme och tid, "Berättade Lehners Phys.org . "Snarare, de nya matematiska förutsättningarna, som vi var tvungna att införa för att undvika instabilitet, kan tolkas som att det redan fanns fluktuationer av rum och tid. Detta är faktiskt vad man kan förvänta sig av kvantteorin i alla fall, eftersom kvantosäkerhetsprincipen innebär att det alltid ska finnas fluktuationer, förmodligen till och med av rum och tid. "
Det nya förslaget kombinerar flera idéer som tidigare har föreslagits för att övervinna problemet med instabilitet. Deras arbete förändrar i huvudsak geometrin i det utrymme över vilket vägintegralen definieras. Vägen integral, som representerar universums tillstånd vid en viss tid, passerar genom vissa kritiska punkter som kallas sadelpunkter, som motsvarar möjliga Hawking-Hartle-stater.
Dock, de flesta av dessa sadelpunkter är instabila. En av de viktigaste förändringarna som fysikerna gjorde i det nya papperet var att ändra gränsförhållandena för hela geometrin (genom att använda Robin -gränsförhållanden) för att ta bort de instabila sadelpunkterna från vägen för integralen. I den nya geometrin, vägintegralen passerar endast genom en sadelpunkt, som är stabil, undviker därför problemet med instabilitet. Vid denna stabila sadelpunkt, det finns en Hawking-Hartle-stat som uppfyller förslaget utan gränser.
Genom att demonstrera en stabil metod för att formulera det gränslösa förslaget, resultaten kan leda till en omprövning av idén som en beskrivning av universums ursprung. Fortfarande, det återstår många frågor.
"I framtiden planerar vi att se hur robust vår nya definition är när vi införlivar aspekter från strängteori, vilket är det mest avancerade försöket till en fullständig teori om kvantgravitation, "Sa Lehners." Också, vi planerar att undersöka om andra stabila definitioner av förslaget utan gräns kan finnas, eller om vår nya i någon mening är unik. Och en stor fråga som återstår är om vi kan härleda några testbara/observerbara konsekvenser. "
© 2019 Science X Network