Ordet osäkerhet används mycket i kvantmekanik. En tankegång är att det här betyder att det finns något där ute i världen som vi är osäkra på. Men de flesta fysiker tror att naturen i sig är osäker.

Inre osäkerhet var central för hur den tyska fysikern Werner Heisenberg, en av upphovsmännen till modern kvantmekanik, presenterade teorin.

Han lade fram osäkerhetsprincipen som visade att vi aldrig kan känna till alla partikels egenskaper samtidigt.

Till exempel, mätning av partikelns position skulle göra det möjligt för oss att veta dess position. Men denna mätning skulle nödvändigtvis störa dess hastighet, med en mängd omvänt proportionell mot positionsmätningens noggrannhet.

Fick Heisenberg fel?

Heisenberg använde osäkerhetsprincipen för att förklara hur mätning skulle förstöra den klassiska egenskapen hos kvantmekanik, det tvåspaltade interferensmönstret (mer om detta nedan).

Men redan på 1990 -talet några framstående kvantfysiker påstod sig ha bevisat att det är möjligt att avgöra vilken av de två slitsarna som en partikel går igenom, utan att väsentligt störa dess hastighet.

Betyder det att Heisenbergs förklaring måste vara fel? I arbete som just publicerades i Science Advances, mina experimentella kollegor och jag har visat att det vore oklokt att hoppa till den slutsatsen.

Vi visar en hastighetsstörning - av den storlek som förväntas av osäkerhetsprincipen - finns alltid, i viss mening.

Men innan vi går in på detaljerna måste vi förklara kort om experimentet med två delar.

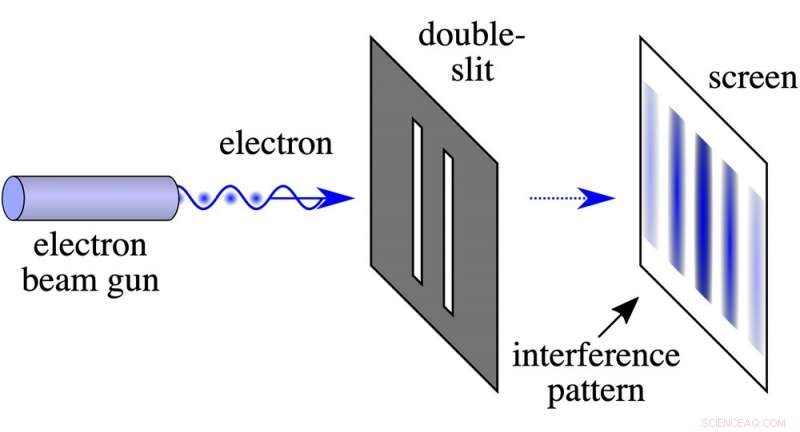
Experimentet med två slitsar

I denna typ av experiment finns det en barriär med två hål eller slitsar. Vi har också en kvantpartikel med en lägesosäkerhet som är tillräckligt stor för att täcka båda slitsarna om den skjuts mot barriären.

Eftersom vi inte kan veta vilken spalt partikeln går igenom, det fungerar som om det går igenom båda slitsarna. Signaturen för detta är det så kallade "interferensmönstret":krusningar i fördelningen av var partikeln sannolikt kommer att hittas vid en skärm i det bortre fältet utanför slitsarna, vilket betyder en lång väg (ofta flera meter) förbi slitsarna.

Men tänk om vi sätter en mätanordning nära barriären för att ta reda på vilken spalt partikeln går igenom? Kommer vi fortfarande att se interferensmönstret?

Vi vet att svaret är nej, och Heisenbergs förklaring var att om positionsmätningen är tillräckligt noggrann för att avgöra vilken slits partikeln går igenom, det kommer att ge en slumpmässig störning av dess hastighet som är tillräckligt stor för att påverka var den hamnar i det bortre fältet, och därmed tvätta bort störningar från krusningarna.

Vad de framstående kvantfysikerna insåg är att för att ta reda på vilken spalt partikeln går igenom inte kräver en positionsmätning som sådan. Varje mätning som ger olika resultat beroende på vilken spalt partikeln går igenom kommer att göra.

Och de kom på en anordning vars effekt på partikeln inte är den av en slumpmässig hastighetsspark när den går igenom. Därav, de bråkade, det är inte Heisenbergs osäkerhetsprincip som förklarar förlusten av störningar, men någon annan mekanism.

Som Heisenberg förutspådde

Vi behöver inte gå in på vad de påstod var mekanismen för att förstöra störningar, eftersom vårt experiment har visat att det har en effekt på partikelns hastighet, av just den storlek Heisenberg förutspådde.

Vi såg vad andra har missat eftersom denna hastighetsstörning inte händer när partikeln går genom mätanordningen. Det dröjer snarare tills partikeln är långt förbi slitsarna, på väg mot det bortre fältet.

Hur är detta möjligt? Väl, eftersom kvantpartiklar egentligen inte bara är partiklar. De är också vågor.

Faktiskt, teorin bakom vårt experiment var en där både våg och partikelnatur är uppenbara - vågen styr partikelns rörelse enligt tolkningen som introducerades av teoretiska fysikern David Bohm, en generation efter Heisenberg.

Låt oss experimentera

I vårt senaste experiment, forskare i Kina följde en teknik som jag föreslog 2007 för att rekonstruera den hypoteserade rörelsen för kvantpartiklarna, från många olika möjliga utgångspunkter över båda slitsarna, och för båda mätresultaten.

De jämförde hastigheterna över tiden när det inte fanns någon mätanordning närvarande med dem när det fanns, och bestämde så förändringen i hastigheterna som ett resultat av mätningen.

Experimentet visade att mätningens effekt på partiklarnas hastighet fortsatte långt efter att partiklarna hade rensat själva mätanordningen, så långt som 5 meter från den.

Vid den punkten, i fjärran, den kumulativa hastighetsförändringen var precis tillräckligt stor, i genomsnitt, att tvätta bort krusningarna i störningsmönstret.

Så, i slutet, Heisenbergs osäkerhetsprincip framträder triumferande.

Meddelandet om att ta hem? Gör inte långtgående påståenden om vilken princip som kan eller inte kan förklara ett fenomen förrän du har övervägt alla teoretiska formuleringar av principen.

Ja, det är lite av ett abstrakt budskap, men det är råd som kan gälla inom områden långt från fysik.

Denna artikel publiceras från The Conversation under en Creative Commons -licens. Läs originalartikeln.