
M81 spiralgalax. Upphovsman:NASA/JPL-Caltech/ESA/Harvard-Smithsonian CfA
Astronomen Johannes Kepler från 1600-talet var den första att fundera över snöflingans struktur. Varför är de så symmetriska? Hur vet en sida hur länge den motsatta sidan har vuxit? Kepler trodde att allt berodde på vad vi nu skulle kalla ett "morfogent fält" - det där vilja att ha den form de har. Vetenskapen har sedan diskonterat denna idé. Men frågan om varför snöflingor och liknande strukturer är så symmetriska förstås ändå inte helt.
Modern vetenskap visar hur grundläggande frågan är:titta på alla spiralgalaxerna där ute. De kan ha en halv miljon ljusår över, men de bevarar fortfarande sin symmetri. Hur? I vår nya studie, publicerad i Vetenskapliga rapporter , presenterar vi en förklaring.
Vi har visat att information och "entropi"-ett mått på störningen i ett system-är sammanlänkade ("info-entropi") på ett sätt exakt analogt med elektriska och magnetiska fält ("elektromagnetism"). Elektriska strömmar producerar magnetfält, medan förändrade magnetfält producerar elektriska strömmar. Information och entropi påverkar varandra på samma sätt.
Entropi är ett grundläggande begrepp inom fysiken. Till exempel, eftersom entropi aldrig kan minska (störningen ökar alltid) kan du göra ett ägg till äggröra men inte tvärtom. Om du flyttar information måste du också öka entropin - ett telefonsamtal har en entropikostnad.
Vi visade att entropi och information kan behandlas som ett fält och att de är relaterade till geometri. Tänk på de två strängarna i DNA -dubbelspiralen som lindar runt varandra. Ljusvågor har samma struktur, där de två strängarna är de elektriska och magnetiska fälten. Vi visade matematiskt att förhållandet mellan information och entropi kan visualiseras med samma geometri.

Riktig snöflinga. Upphovsman:Karen Schanely:https://www.clickinmoms.com/blog/take-macro-snowflakes-pictures/; allmängods
Vi ville se om vår teori kunde förutsäga saker i den verkliga världen, och bestämde sig för att försöka beräkna hur mycket energi du behöver för att omvandla en form av DNA till en annan. DNA är trots allt en spiral och en form av information.
Detta gjordes faktiskt i utomordentligt exakta mätningar för cirka 16 år sedan. Forskarna drog en DNA -molekyl rakt (DNA gillar att krypa ihop), och snodde det 4, 800 varv medan du håller ändarna med en optisk pincett. DNA vänds från en form till en annan, som på bilden ovan. Forskarna kunde sedan beräkna energiskillnaden mellan de två formerna.
Men vår teori kan beräkna denna energiskillnad, för. Vi kände entropin för var och en av de två versionerna av denna DNA -molekyl, och energin är helt enkelt produkten av entropi och temperatur. Vårt resultat var perfekt - teorin tycktes hålla.
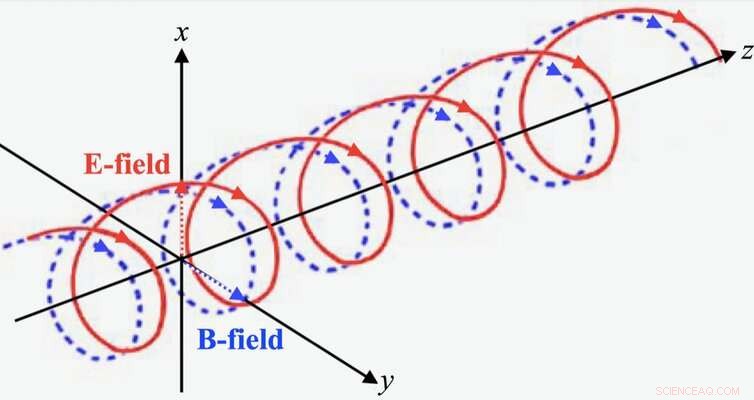
Ljusvåg med elektriska (E) och magnetiska (B) fält. Författare tillhandahålls
Från liten till enorm
Spiralgalaxer är dubbla spiraler precis som DNA är en dubbel helix - matematiskt sett har de liknande geometrier.
Vår teori visar direkt varför spiralgalaxernas två armar är symmetriska-det beror på att info-entropifält ger upphov till krafter (som andra fält). Stjärnorna i galaxen koreograferas helt enkelt av en entropisk kraft för att radas upp i ett par sådana spiraler för att maximera entropin.
Men vi ville få några riktiga siffror, för. Vi bestämde oss därför för att försöka beräkna massan av vår galax från vår teori. Vi vet hur tung Vintergatan verkar vara från hur snabbt stjärnorna rör sig nära den galaktiska kanten - det är cirka 1,3 biljoner solmassor.
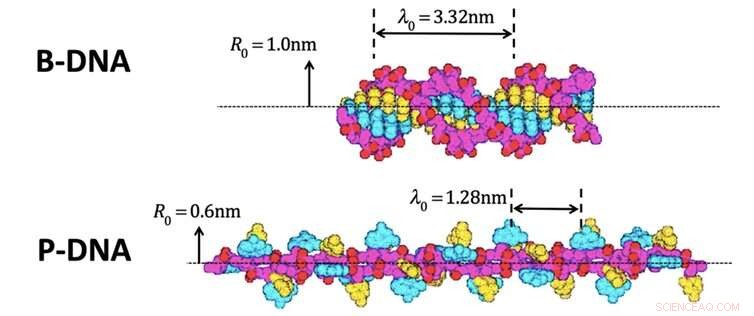
Två former av DNA. Upphovsman:Parker &Jeynes, Fig.1 i vetenskapliga rapporter 9 | 10779 (2019); Modifierad från fig. 5 i Allemand et al. Proc. Natl. Acad. Sci. USA 95, 14152–14157 (1998), CC BY
Underligt, detta är faktiskt mycket mer än massan av alla synliga stjärnor i galaxen. För att kunna förklara denna skillnad och redogöra för varför stjärnor rör sig så mycket snabbare än förväntat, astronomer kom på idén om "mörk materia" - osynlig massa som lurar i galaxen, öka sitt gravitationstryck på stjärnorna.
Vi behövde känna till galaxens entropi för våra beräkningar. Lyckligtvis, den matematiska fysikern Roger Penrose visade att denna entropi domineras av entropin i dess centrala supermassiva svarta hål.
Vi vet massan av detta svarta hål (4,3 m solmassor). Och otroligt, när du vet massan av ett svart hål, det finns en ekvation, upptäckt av avlidne fysikern Stephen Hawking, som beräknar dess entropi. Hawking upptäckte också hur man beräknar "temperaturen" vid dess yta, eller "händelsehorisont".
Om du kan tilldela en "temperatur" till det svarta hålets händelsehorisont - som inte har saker i sig för att ha temperatur - varför inte också tilldela en temperatur till en galax? Vi hävdar i vårt papper att detta är rimligt (med hjälp av det som kallas "holografisk princip"). Så vi använde våra info-entropiekvationer för att beräkna galaxens holografiska temperatur.

En spiralgalax med en överlagrad dubbelarmad logaritmisk spiral. Upphovsman:Parker &Jeynes, Bild 2 av Vetenskapliga rapporter 9 | 10779 (2019), CC BY-SA
Då blir det lätt. Vi vet att galaktisk energi ges av produkten av dess entropi och temperatur. Och när vi känner till energin kan vi ta reda på massan tack vare Einsteins berömda ekvation:E =mc 2 .
Den här gången var resultatet inte direkt på plats, men det var ganska nära med tanke på vår mycket förenklade modell av galaxen. Den info-entropiska geometrin i en galax förklarar inte bara hur entropiska krafter skapar den vackert symmetriska formen och behåller den, men står också för all massa som tycks vara tydlig i den.
Det betyder att vi faktiskt inte behöver mörk materia trots allt. Enligt vår modell, den galaktiska entropin ger upphov till en så stor mängd extra energi att den modifierar den observerade dynamiken i galaxen - vilket gör att stjärnor vid kanten rör sig snabbare än förväntat. Detta var precis vad mörk materia var tänkt att förklara. Energin är inte direkt observerbar som massa, men dess närvaro stöds verkligen av de astronomiska observationerna - förklarar varför sökningar i mörk materia hittills inte har hittat något.
Det finns dock mycket forskning som stöder tanken på mörk materia. Vår teori föreslår en alternativ förklaring av observationerna, och behöver ingen ny fysik. Självklart, mer detaljerat arbete behövs för att verifiera att observationernas sanna komplexitet också kan modelleras framgångsrikt.
Vi tror att det "morfogena fält" som Kepler sökte verkligen existerar, och är faktiskt effekten av sammanflätning av information och entropi. Efter fyra långa århundraden, det verkar som om Kepler äntligen har fått rätt.
Denna artikel publiceras från The Conversation under en Creative Commons -licens. Läs originalartikeln. 