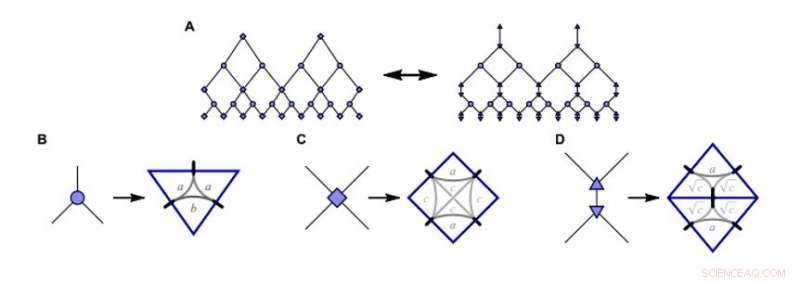
Konstruera matchporten MERA (multiscale entanglement renormalization ansatz simulation; mMERA) leksaksmodell. A:Standard MERA tensornätverk (vänster) i den numeriska matchgate-inställningen för studien motsvarar B-D:Isometries, disentanglers, och triangulerade disentanglers (från vänster till höger) uttryckt som matchgate -tensorer. De fria parametrarna a, b, c fixa komponenterna i genereringsmatriserna. Upphovsman:Science Advances, doi:10.1126/sciadv.aaw0092
Tensornätverk har en central roll i kvantfysiken eftersom de kan ge en effektiv approximation till specifika klasser av kvanttillstånd. Det associerade grafiska språket kan också enkelt beskriva och bildmässigt resonera om kvantkretsar, kanaler, protokoll och öppna system. I en nyligen genomförd studie A. Jahn och ett forskargrupp vid avdelningarna för komplexa kvantsystem, material och energi och matematik och datavetenskap i Tyskland introducerade en mångsidig och effektiv ram för att studera tensornätverk genom att utöka tidigare verktyg. Forskarna använde bulkplattor (datorgeometrisk teknik) i sitt arbete för att få mycket exakta kritiska data och etablerade en koppling mellan holografiska kvantfelkorrigerande koder och tensornätverk. De förväntar sig att arbetet kommer att stimulera ytterligare undersökningar av tensornätverksmodeller för att fånga bulkgränskorrespondenser. Resultaten publiceras nu den Vetenskapliga framsteg .
AdS/CFT -korrespondensen, som står för anti-de Sitter/conformal field theory correspondence, är ett av de största forskningsområdena inom strängteori, och är ett exempel i samband med bulkgränsdualiteter där en holografisk dualitet existerar mellan gravitationen i ett bulkrum och ett kritiskt kvantfält på dess gräns. Denna korrespondens som handlar om två mycket olika teorier formulerades ursprungligen av fysikern Juan M. Maldacena 1997, och anses vara ett betydande viktigt resultat inom strängteori under de senaste 20 åren.
En nyckelfunktion i dessa dualiteter är förhållandet mellan bulkgeometri och gränsen entanglement entropies, som fysiker tidigare hade belyst med Ryu-Takayanagi-formeln. Eftersom det är viktigt att förstå intrassling i samband med AdS/CFT, forskare insåg nödvändigheten av tensornätverk som en idealisk ram för att konstruera holografiska leksaksmodeller, till exempel multiscale entanglement renormalization ansatz simulation (MERA). Fysiker hade tidigare utforskat insikten om att kvantfelkorrigering kan underlättas av en holografisk dualitet, som vidare kopplade till idéer från kvantinformationsteori. Även om forskare framgångsrikt konstruerade flera tensornätverksmodeller för att återge en mängd aspekter på AdS/CFT, de saknade fortfarande en allmän förståelse för egenskaperna och gränserna för tensornätverksholografi. Specifika hinder för processen inkluderar de potentiellt stora parameterutrymmena för tensornätverk och de betydande beräkningskostnaderna.
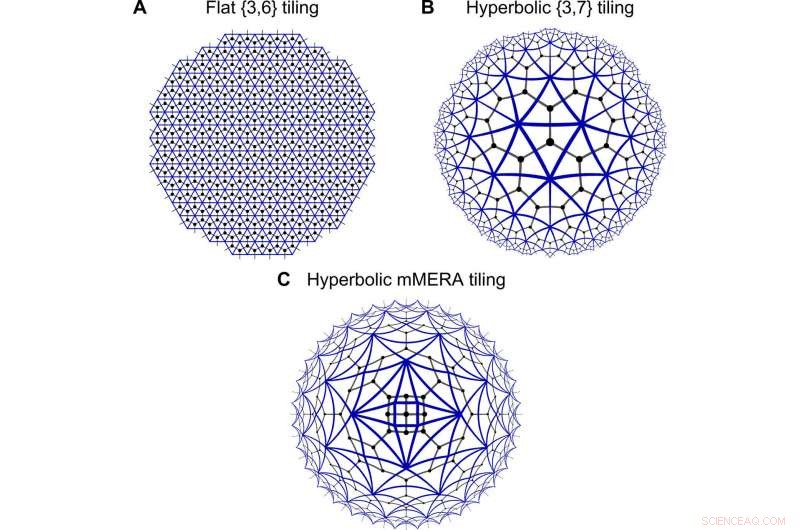
Geometrier hos tensornätverk. Diskretiseringar av platt (A) och hyperboliskt utrymme (B och C) med en triangulär kakel (blå kanter), i vilket ett tensornätverk är inbäddat (svart gitter). I matchportens formalism, skarvkanter mellan trianglar motsvarar en integration över ett par Grassmann -nummer, analogt med tensors nätverkskontraktion över index. Medan (A) och (B) visar vanliga plattor, (C) presenterar en oregelbunden MERA-liknande kakel, som forskarna namngav tändsticksluckan MERA (mMERA). Upphovsman:Science Advances, doi:10.1126/sciadv.aaw0092
I det nuvarande arbetet, Jahn et al. övervann de befintliga utmaningarna genom att tillämpa mycket effektiva kontraktionstekniker utvecklade av matchgate -tensorer. De mångsidiga teknikerna gjorde det möjligt för forskargruppen att på ett omfattande sätt studera samspelet mellan geometri och korrelationer i gaussiska fermioniska tensornätverk genom att införliva leksaksmodeller för kvantfelkorrigering. De inkluderade också tidigare tensornätverk som "MERA" -modellen inom det nuvarande arbetet, för att markera samband mellan dem. Teamet begränsade studien till tensornätverk som är oeniga och verkliga, liknar en euklidisk utveckling från massan till gränsen. Jahn et al. tillhandahållit nya tillvägagångssätt i samband med renormalisering av tensornätverk, att styrka tensornätens förmåga att beskriva bulkgränsöverensstämmelser bortom kända modeller. Föreliggande arbete är preliminärt och ger en utgångspunkt för mer systematiska studier om holografi i tensornätverk.
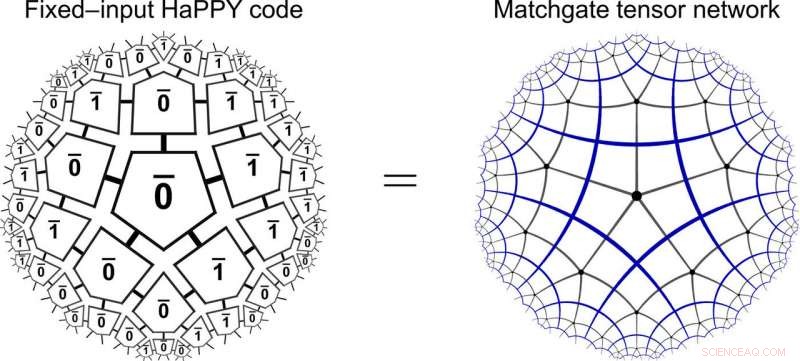
HaPPY/matchgate -ekvivalens. Den holografiska pentagonkoden för HaPPY -modellen för fast beräknad bulkingång (vänster) är lika med ett matchgate -tensornätverk på ett hyperboliskt pentagonplattor (höger). Upphovsman:Science Advances, doi:10.1126/sciadv.aaw0092
Forskarna tillämpade först sitt ramverk på den högsymmetriska klassen vanliga bulkplattor för att implementera den holografiska felkorrigerande koden (HaPPY -kod) som föreslås någon annanstans. Därefter, de undersökte mångsidigheten i ramverket för att utvidga det mot mer fysiska inställningar. De använde först HaPPY -kodleksaksmodellen för att förstå bulk/gräns -korrespondensen med bulkplattor av holografiska pentagoner, där varje femkantskakel kodade en fel-tolerant logisk qubit. I korthet, forskargruppen observerade att fastställande av större frihetsgrader till beräkningsbaserade tillstånd kan ge upphov till en matchgate -tensornätverk. De visade att beräkningsgrundstaterna var rena Gaussiska och drog slutsatsen att för fast beräkningsmängd i bulk, den holografiska pentagramkoden kan ge en matchgate -tensor på gränsen. Använda en Schläfli -symbol {p, q} där p =antalet kanter per polygon och q =antalet polygoner runt varje hörn, de specificerade den hyperboliska geometrin för HaPPY -modellen.
Efter att Jahn et al. visade att deras modellramar inkluderade den holografiska pentagonkoden byggd från fem-qubit stabilisatorstater för fasta bulkinmatningar. De visade att gränstillstånden motsvarar icke -lokal bulkparning med exotiska partiklar som kallas Majorana fermioner. Arbetet öppnade alltså en väg för att studera de statliga egenskaperna hos en holografisk modell i stora storlekar. Forskarna beräknade vidare tvåpunktskorrelatorerna och förträngningens entropier i systemet. De visade sedan att de kritiska och gappade gaussiska gränsstaterna kunde realiseras bortom kända modeller med hjälp av olika bulkplattor. I föreliggande arbete återgav de de genomsnittliga skalningsegenskaperna för Ising CFT (conformal field theory) leksaksmodell; enklaste möjliga modellen i teoretisk fysik som möjliggjorde metoder för euklidisk kvantfältteori och studier av kritiska fenomen.
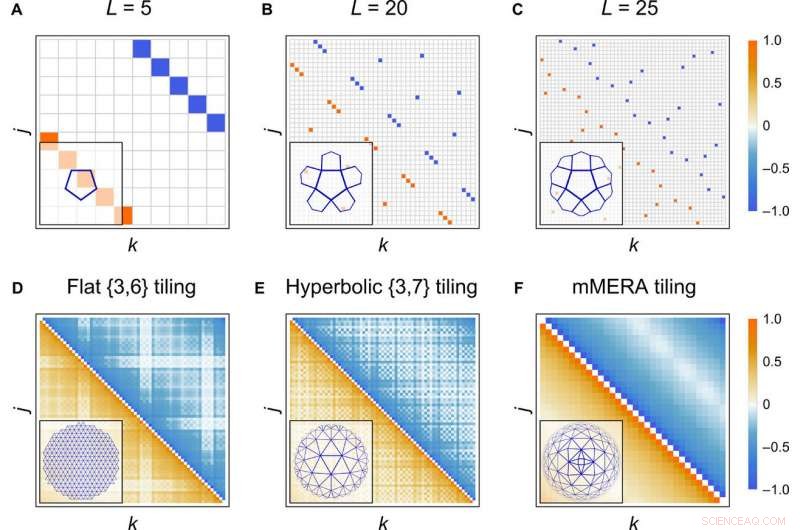
Gränstillståndskorrelationer. (A till C) Majorana kovariansmatris Γ med färgkodade poster för ett gränsläge för en hyperbolisk {5, 4} plattsättning av HaPPY -koden med fast 0¯ -ingång på varje kakel. Gränsen består av 2L =10, 40, och 50 Majorana -platser, respektive. (D till F) Fältkorrelationsmatris 〈ψjψk - ψkψj〉/2 =(Γ2j, 2k − 1 + Γ2j − 1, 2k)/4 för gränstillstånd för {3, 6}, {3, 7}, och mMERA -plattsättning vid kritikalitet med L =63, 69, och 64 gränsplatser, respektive. Matrisposter normaliseras till samma färgskala. Kaklet som motsvarar varje korrelationsmatris i (A) till (F) visas i nedre vänstra hörnet. Upphovsman:Science Advances, doi:10.1126/sciadv.aaw0092
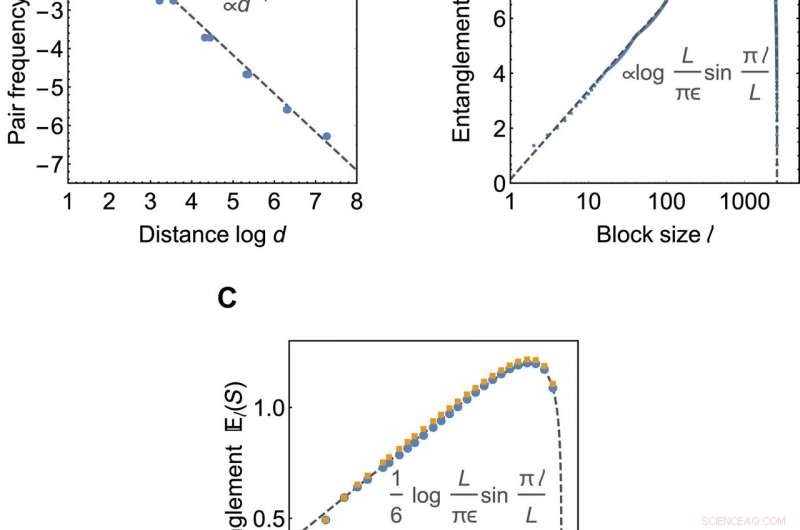
Kritiska korrelationer och trasselskalning. (A och B) Gränslägeegenskaper för HaPPY -koden vid 2605 gränsplatser. (A) visar genomsnittliga korrelationer vid gränsavstånd d, beräknas som den relativa frekvensen n för Majorana -par. Streckad grå linje visar en n (d) ~ 1/d numerisk passform. (B) visar skalning av genomsnittlig intrassling entropi El (S) med delsystemstorlek l. Streckad grå linje visar numerisk passform med (11). (C) El (S) för regelbundna plattor vid de kritiska värdena a =0,580 för en {3, 6} kakel (blå) och vid a =0,609 för {3, 7} kakel (gul) med 348 gränsplatser vardera. Den streckade grå linjen visar den exakta c =1/2 CFT -lösningen. Upphovsman:Science Advances, doi:10.1126/sciadv.aaw0092
Jahn et al. byggde sedan ett euklidiskt matchgate tensornätverk baserat på den tidigare utvecklade MERA -geometrin och kallade det matchgate MERA (mMERA). Denna kakelinvarians som de uttryckte som en triangulering (flera åtgärder för att fånga en konstruktion), återställde Ising CFT med små beräkningskostnader. Beräkningsoptimeringsprocessen i studien tog bara några minuter på en stationär dator för ett nätverk med hundratals tensorer.
På det här sättet, A. Jahn och kollegor introducerade ett effektivt preliminärt ramverk för att studera tensornätverk och föreslog ytterligare studier inom den gaussiska inställningen för att fokusera på positivt böjda bulks, modeller med högre dimension och slumpmässiga tensorer. Ytterligare studier bortom Gaussianity kan utforska interagerande fermioniska tensornätverk genom svag kopplingsexpansion eller under lokalt begränsade interaktioner. Båda de föreslagna möjliga utökningarna av det ramverk som presenteras i studien kommer bara att kräva beräkningskalningspolynom till systemstorleken för att undvika oöverkomliga beräkningsinsatser av allmänna metoder för att extrahera tensorkontraktion.
© 2019 Science X Network