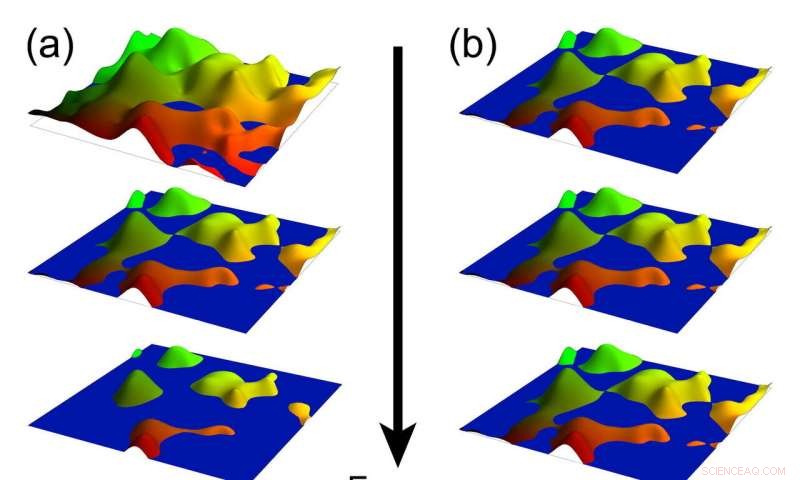
De robusta landskapen i dessa illustrationer visar den elektriska potentialen på ytan av 2D-material som uppvisar kvanthalleffekten. Graden av robusthet motsvarar föroreningar i systemet, och vattennivån representerar "Fermi-energin, ” eller fyllnadsnivå av elektroner. I kvanthalleffekten (vänster), perkolationströskeln (mitten) är ett finjusterat energitillstånd som markerar övergången till topologisk ordning. Ny forskning av fysiker vid Rice University, University of California Berkeley och Karlsruhe Institute of Technology har hittat "staplar" av detta speciella 2D-tillstånd som skyddar mönster av kvantintrassling (höger) genom hela ytenergispektrumet för 3D-topologiska material. Kredit:M. Foster/Rice University
Amerikanska och tyska fysiker har hittat överraskande bevis för att ett av de mest kända fenomenen inom modern fysik – kvant-Hall-effekten – är "reinkarnerad" i topologiska supraledare som skulle kunna användas för att bygga feltoleranta kvantdatorer.
Upptäckten 1980 av quantum Hall-effekten startade studiet av topologiska ordningar, elektroniska tillstånd med "skyddade" mönster av långväga quantum intrassling som är anmärkningsvärt robusta. Stabiliteten i dessa skyddade stater är extremt attraktiv för kvantberäkning, som använder kvantentanglement för att lagra och bearbeta information.
I en studie publicerad online denna månad i Fysisk granskning X ( PRX ), teoretiska fysiker från Rice University, University of California, Berkeley (UC Berkeley), och Karlsruhe Institute of Technology (KIT) i Karlsruhe, Tyskland, presenterade starka numeriska bevis för en överraskande koppling mellan 2-D och 3-D faser av topologisk materia. Kvant Hall-effekten upptäcktes i 2D-material, och laboratorier över hela världen är i en kapplöpning om att göra 3-D topologiska supraledare för kvantberäkning.
"I detta arbete har vi visat att en viss klass av 3-D topologiska supraledare bör uppvisa "energistackar" av 2-D elektroniska tillstånd på sina ytor, " sa Rice medförfattare Matthew Foster, en docent i fysik och astronomi och medlem av Rice Center for Quantum Materials (RCQM). "Var och en av dessa staplade tillstånd är en robust 'reinkarnation' av en enda, mycket speciellt tillstånd som inträffar i 2D-kvanthalleffekten."
Kvant Hall-effekten mättes först i tvådimensionella material. Foster använder en "percolation"-analogi för att visualisera de konstiga likheterna mellan vad som sker i 2-D kvanthall-experiment och studiens 3-D-beräkningsmodeller.
"Föreställ dig ett pappersark med en karta över oländiga toppar och dalar, och föreställ dig sedan vad som händer när du fyller landskapet med vatten, " sa han. "Vattnet är våra elektroner, och när vätskenivån är låg, du har bara isolerade sjöar av elektroner. Sjöarna är bortkopplade från varandra, och elektronerna kan inte leda över huvuddelen. Om vattennivån är hög, du har isolerade öar, och i det här fallet är öarna som elektronerna, och du får inte heller bulkledning."
I Fosters analogi är det robusta landskapet den elektriska potentialen hos 2D-materialet, och nivån av robusthet motsvarar mängden föroreningar i systemet. Vattennivån representerar "Fermi-energin, " ett koncept inom fysiken som hänvisar till fyllnadsnivån för elektroner i ett system. Kanterna på papperskartan är analoga med 1D-kanterna som omger 2D-materialet.
"Om du tillsätter vatten och justerar vätskenivån exakt till den punkt där du har små broar av vatten som förbinder sjöarna och små broar av land som förbinder öarna, då är det lika lätt att resa till vatten eller land, " sa Foster. "Det är tröskeln för perkolation, vilket motsvarar övergången mellan topologiska tillstånd i quantum Hall. Detta är det speciella 2D-tillståndet i quantum Hall.
"Om du ökar vätskenivån mer, nu är elektronerna fångade på isolerade öar, och man skulle tro, 'Väl, Jag har samma situation som jag hade tidigare, utan ledning.' Men, vid den särskilda övergången, ett av de elektroniska tillstånden har skalat bort till kanten. Att tillsätta mer vätska tar inte bort kanttillståndet, som kan gå runt hela provet, och ingenting kan stoppa det."
Analogin beskriver förhållandet mellan robust kantledning och bulkfinjustering genom den speciella övergången i kvanthalleffekten. I PRX-studien, Foster och medförfattare Björn Sbierski från UC Berkeley och Jonas Karcher från KIT studerade 3D-topologiska system som liknar 2D-landskapen i analogin.
"Det intressanta i dessa 3D-system händer också bara vid gränsen, " sa Foster. "Men nu är våra gränser inte 1D-kanttillstånd, de är 2D-ytor."
Genom att använda "brute-force numeriska beräkningar av yttillstånden, "Sbierski, Karcher och Foster hittade en koppling mellan det kritiska 2-D kvantum Hall-tillståndet och 3-D-systemen. Liksom 1D-kanttillståndet som kvarstår ovanför övergångsenergin i 2D-kvanthallmaterial, beräkningarna avslöjade ett ihållande 2D-gränstillstånd i 3D-systemen. Och inte vilket 2D-tillstånd som helst; det är exakt samma 2D-perkolationstillstånd som ger upphov till 1D kvanthall-kanttillstånd.
"Det som var en finjusterad topologisk kvantfasövergång i 2-D har "reinkarnerats" som det generiska yttillståndet för en högre dimensionell bulk, " sa Foster. "I 2018 års studie, min grupp identifierade en analog koppling mellan en annan, mer exotisk typ av 2-D kvant Hall-effekt och yttillstånden för en annan klass av 3-D topologiska supraledare. Med dessa nya bevis, vi är nu övertygade om att det finns en djup topologisk orsak till dessa kopplingar, men för tillfället förblir matematiken obskyr."
Topologiska supraledare har ännu inte realiserats experimentellt, men fysiker försöker skapa dem genom att lägga till föroreningar till topologiska isolatorer. Denna process, känd som doping, har använts i stor utsträckning för att tillverka andra typer av okonventionella supraledare från bulkisolatorer.
"Vi har nu bevis för att tre av de fem 3-D topologiska faserna är bundna till 2-D faser som är versioner av kvant-Hall-effekten, och alla tre 3D-faserna skulle kunna realiseras i 'topologiska supraledare, sa Foster.
Foster sa att den konventionella visdomen inom den kondenserade materiens fysik har varit att topologiska supraledare var värd endast ett skyddat 2-D yttillstånd och alla andra tillstånd skulle påverkas negativt av oundvikliga brister i de fasta material som används för att tillverka supraledarna.
Men Sbierski, Karcher och Fosters beräkningar tyder på att så inte är fallet.
"I Quantum Hall, du kan ställa in var som helst och fortfarande få denna robusta platå i konduktans, på grund av 1D-kanttillstånden, " Foster sa. "Vårt arbete tyder på att det också är fallet i 3D. Vi ser högar av kritiska tillstånd på olika energinivåer, och alla av dem är skyddade av denna märkliga reinkarnation av 2D-kvant Hall-övergångstillståndet."
Författarna satte också scenen för experimentellt arbete för att verifiera sina resultat, utarbeta detaljer om hur yttillstånden för 3D-faserna ska se ut i olika experimentella sonder.
"Vi tillhandahåller exakta statistiska "fingeravtryck" för yttillstånden i de topologiska faserna, Foster sa. "De faktiska vågfunktionerna är slumpmässiga, på grund av oordning, men deras distributioner är universella och matchar kvanthallövergången."