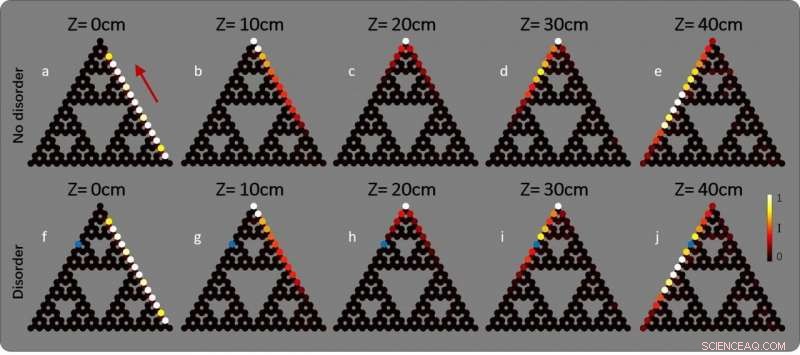
a-e Utveckling av topologiska kanttillstånd i det fraktala SG(4)-gittret. en Intensitetsfördelning av det initiala fältet konstruerat från ett trunkerat topologiskt kanttillstånd i fraktalgittret. b-e Intensitetsfördelning vid fortplantningsavstånd . f-j Evolution i fraktalgittret som innehåller störningar på plats av , vars position markeras av den blå pricken. Vågpaketet visar topologiskt skyddad kanttransport runt hörnen och påverkas inte av störningen. Färgfältet indikerar fältets intensitet. Upphovsman:av Zhaoju Yang, Eran Lustig, Yaakov Lumer och Mordechai Segev
Topologiska isolatorer är en ny fas av materia som är unik för sin isolerande bulk och perfekt ledande kanter. De har legat i framkanten av den kondenserade materiens fysik under det senaste decenniet, och mer nyligen inspirerade uppkomsten av topologiska faser i många klassiska vågsystem, såsom fotonik och akustik. Hittills, alla studier av topologiska isolatorer har undersökt system i heltalsdimensioner (fysiskt, 2-D eller 3-D) med en väldefinierad bulk och kanter. Dock, fysiska dimensioner definierar inte alltid de dimensioner som ett system utvecklas i:Vissa strukturer har en icke -hel (fraktal) dimension, trots att du befinner dig i en 2D- eller 3D-sfär.
I en ny tidning publicerad i Ljusvetenskap och applikationer , ett team av forskare, ledd av professor Mordechai Segev från fysikavdelningen och Solid State Institute, Technion-Israel Institute of Technology, Israel, och medarbetare har utvecklat den fotoniska Floquet topologiska isolatorn i ett periodiskt driven fraktalt gitter. Detta gitter förlitar sig på en fraktal fotonisk kristall [Sierpinski-packningen (SG)] som består av evanescent kopplade spiralformade vågledare, vilket kan realiseras med femtosekund-laser-skrivteknik. De beräknar det topologiska Floquet-spektrumet och visar förekomsten av topologiska kanttillstånd som motsvarar Chern nummer 1 i det verkliga rymden. Simuleringarna av kanttillstånden visar att vågpaket som består av topologiska kanttillstånd kan fortplanta sig längs de yttre och inre kanterna utan att tränga in i "bulk" och utan bakåtspridning även i närvaro av oordning och skarpa hörn.
"Våra resultat tyder på en mängd nya typer av topologiska system och nya tillämpningar, som att använda topologisk robusthet kombinerat med den ökade känsligheten hos fraktala system för avkänning och, i icke-ermitiska miljöer, topologiska isolatorlasrar i fraktala dimensioner, ", förutspår forskarna.