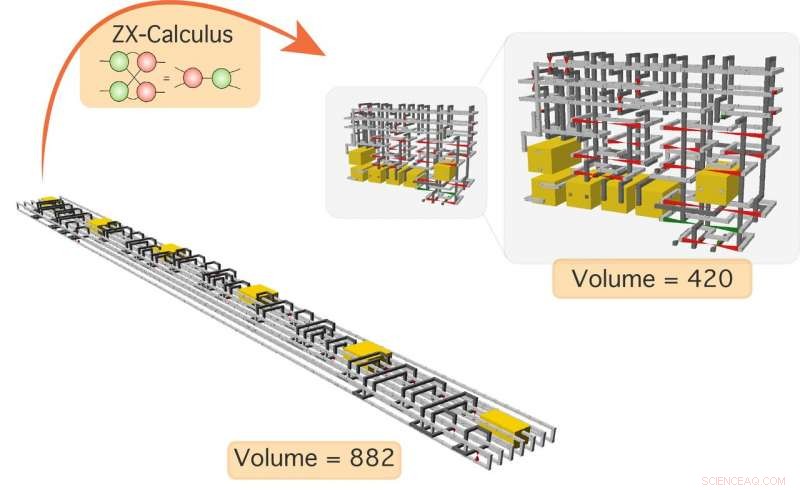
Komprimering av en krets som har en initial volym på 882 med den föreslagna metoden. Den reducerade kretsen har en volym på 420, mindre än hälften av dess ursprungliga volym. Kredit:National Institute of Informatics
En stor teknisk utmaning för alla praktiska, den verkliga kvantdatorn kommer från behovet av ett stort antal fysiska qubits för att hantera fel som ackumuleras under beräkningen. Sådan kvantfelskorrigering är resurskrävande och beräkningsmässigt tidskrävande. Men forskare har hittat en effektiv mjukvarumetod som möjliggör betydande komprimering av kvantkretsar, lätta på kraven på hårdvaruutveckling.
Kvantdatorer kan fortfarande vara långt ifrån en kommersiell verklighet, men vad som kallas "kvantfördelar" - förmågan hos en kvantdator att beräkna hundratals eller tusentals gånger snabbare än en klassisk dator - har verkligen uppnåtts på vad som kallas Noisy Intermediate-Scale Quantum (NISQ)-enheter i tidiga bevis-av -principella experiment.
Tyvärr, NISQ-enheter är fortfarande utsatta för massor av fel som ackumuleras under deras drift. För att det ska finnas någon verklig tillämpning av kvantfördelar, designen av en fullt fungerande storskalig kvantdator med hög feltolerans krävs. För närvarande, NISQ-enheter kan konstrueras med cirka 100 qubits, men feltoleranta datorer skulle åtminstone behöva miljontals fysiska qubits för att koda den logiska informationen med tillräckligt låga felfrekvenser. En feltolerant implementering av kvantberäkningskretsar gör inte bara kvantdatorn större, men också körtiden längre i storleksordningar. En utökad körtid innebär i sin tur att beräkningen är ännu mer känslig för fel.
Även om framsteg inom hårdvara kan åtgärda denna resursklyfta, forskare från National Institute of Informatics (NII) och Nippon Telegraph and Telephone Corporation (NTT) i Japan tacklade problemet från mjukvaruutvecklingssidan genom att komprimera kvantkretsar i storskaliga feltoleranta kvantdatorer, potentiellt minska behovet av hårdvaruförbättringar.
"Genom att komprimera kvantkretsar, vi skulle kunna minska storleken på kvantdatorn och dess körtid, vilket i sin tur minskar kravet på felskydd, sa Michael Hanks, en forskare vid NII och en av författarna till en artikel, publicerad 11 november i Fysisk granskning X .
Storskaliga kvantdatorarkitekturer är beroende av en felkorrigeringskod för att fungera korrekt, den vanligaste är ytkod och dess varianter.
Forskarna fokuserade på kretskomprimeringen av en av dessa varianter:den 3-D-topologiska koden. Den här koden beter sig särskilt bra för distribuerade kvantdatormetoder och har bred tillämpbarhet på olika typer av hårdvara. I den 3-D-topologiska koden, kvantkretsar ser ut som sammanflätade rör eller rör, och kallas vanligtvis "flätade kretsar. 3D-diagrammen för flätade kretsar kan manipuleras för att komprimera och därmed minska volymen de upptar. Fram till nu, utmaningen har varit att sådan "rörmanipulation" utförs på ett ad hoc-sätt. Dessutom, det har bara funnits partiella regler för hur man gör detta.
"Tidigare komprimeringsmetoder kan inte garantera om den resulterande kvantkretsen är korrekt, " sa medförfattaren Marta Estarellas, en forskare vid NII. "Man måste vara mycket noga med att kontrollera dess korrekthet varje gång en av dessa komprimeringsregler tillämpas. Detta är en viktig fråga, eftersom en sådan uppgift är lika svår som att köra hela kvantkretsen."
Forskargruppen föreslår användningen av ZX-kalkyl som ett språk för detta mellanstadium av sammanställning. ZX-calculus är ett 2D-diagramspråk (med diagram och bilder istället för ord) utvecklat i slutet av 2000-talet uttryckligen för att möjliggöra en intuitiv representation av qubit-processer. Mer viktigt, den kommer med en komplett uppsättning manipulationsregler.
I deras papper, forskarna utnyttjar ZX-kalkyl genom att upptäcka translationsrelationerna mellan ZX-kalkyl och komponenterna i den flätade kretsen. Forskarna har visat att dessa två representationer av logiska grindkretsar kan mappas till varandra genom att identifiera en ny tolkning som hela tiden varit gömd i ZX-kalkylen.
ZX-kalkylspråket kan tillämpa en uppsättning transformationsregler för att ändra kretsens struktur utan att ändra dess underliggande matematiska betydelse (och därmed dess funktion) och därför säkerställa dess korrekthet. Genom att noggrant ändra den konceptuella strukturen, kretsens volym kan minimeras, uppnå avsevärda kompressionshastigheter när denna nya struktur är mappad till den faktiska flätade kvantkretsen.
Genom att tillämpa denna teknik, forskarna rapporterar kompressionsminskningar på upp till 77 procent, motsvarande 40 procents minskning jämfört med de bästa tidigare insatserna.
"Kompressionsmetoden och dess vidareutveckling skulle kunna leverera realisering av en verklig feltolerant kvantdator år före schemat, sade William J. Munro, en forskare vid NTT, som också bidragit till forskningen.
"Intressant, det kan också vara grunden för framtida operativsystemutveckling, sa Kae Nemoto, Direktör för Global Research Centre for Quantum Information Science vid NII. "Det kan fortfarande ta många år för denna mjukvaruutveckling att implementeras i fullt skalbara kvantdatorer, men vår metod kan spara en hel del ansträngning i samband med hårdvaruutveckling under tiden."