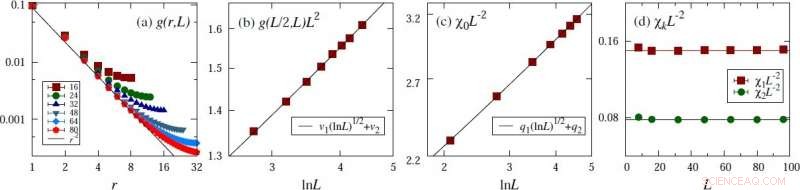
Bevis för den gissade skalningsformen i exemplet med den kritiska 4D XY -modellen. (a) Tvåpunkts korrelationsfunktion. (b) Tvåpunktskorrelation på avståndet till hälften av den linjära systemstorleken. (c) Magnetisk känslighet. (d) Magnetiska fluktuationer vid Fourier-lägen som inte är noll. Upphovsman:© Science China Press
Sedan inrättandet av renormaliseringsgruppsteorin har det har varit känt att system med kritiska fenomen vanligtvis har en övre kritisk dimension dc (dc =4 för O (n) -modellen), så att i rumsliga dimensioner vid eller högre än DC, det termodynamiska beteendet styrs av kritiska exponenter som tar medelvärdesfältvärden. I motsats till enkelheten i det termodynamiska beteendet, teorin om ändlig skalning (FSS) för d> dc O (n) -modellen var förvånansvärt subtil och hade förblivit föremål för pågående debatt tills nyligen, när en två-längdskalningsansatz för tvåpunktskorrelationsfunktionen gissades, numeriskt bekräftat, och delvis stödd av analytiska beräkningar.
Vid den övre kritiska dimensionen dc, multiplikativa och additiva logaritmiska korrigeringar uppträder i allmänhet på det genomsnittliga fältets beteende. Förtydligandet av logaritmiska korrigeringar i FSS blir 'notoriskt svårt, 'på grund av bristen på analytisk insikt bortom den fenomenologiska nivån och gränsen för systemstorlekar som finns tillgängliga i numeriska simuleringar. Den exakta logaritmiska FSS-formen vid d =dc har förblivit ett långvarigt problem.
Nyligen, Jian-Ping Lv, Wanwan Xu, och Yanan Sun från Anhui Normal University, Kun Chen från Rutgers, State University of New Jersey, och Youjin Deng från University of Science and Technology of China och Minjiang University tog upp logaritmiska FSS för O (n) symmetri vid den övre kritiska dimensionen. Låna insikter från högre dimensioner, de etablerade en tydlig skalningsform för den fria energitätheten, som samtidigt består av en skalningsterm för den gaussiska fixpunkten och en annan term med multiplikativa logaritmiska korrigeringar. Särskilt, de gissade att den kritiska tvåpunktskorrelationen med begränsad storlek uppvisar ett beteende i två längder, som styrs av Gauss fixpunkt på kortare avstånd, och går in på en platå på större avstånd vars höjd minskar med systemstorlek i en kraftlag som korrigeras av en logaritmisk exponent.
Utifrån detta, FSS av olika makroskopiska mängder förutspåddes. De genomförde sedan omfattande Monte Carlo-simuleringar för n-vektormodellen med n =1, 2, 3, och erhållit fasta bevis som stöder de gissade skalningsformerna från FSS om känsligheten, de magnetiska fluktuationerna vid icke-noll Fourier-lägen, Bindaren kumulativ, samt tvåpunktskorrelationen på avståndet till hälften av den linjära systemstorleken. Detta är ett viktigt steg mot en komplett lösning av det logaritmiska FSS vid d =dc för system med en övre kritisk dimension.
Studien är inte bara av teoretisk betydelse i modellsystem utan också av praktisk relevans för ett stort antal experimentella system. Det noteras att på grund av den tekniska utvecklingen, den experimentella förverkligandet av O (n) -modellen är nu tillgänglig i olika fysiska system inklusive kvantmagnetiska material, Josephson junction arrays, och ultrakylda atomsystem. Enligt kvant-till-klassisk kartläggning, de tredimensionella kvant O (n) -systemen har den övre kritiska dimensionen.