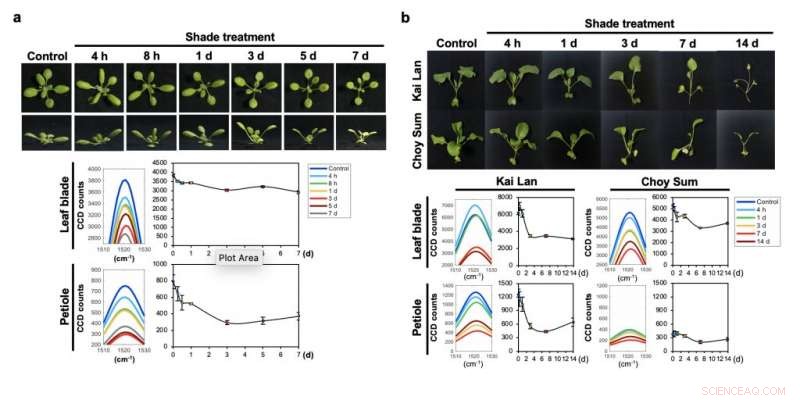
Ramanspektroskopi och karotenoiden Raman-toppen möjliggör tidig upptäckt av Shade Avoidance Syndrome (SAS) i (a) modellväxten Arabidopsis thaliana och (b) bladgrönsaker. Kredit:Kai Lan och Choy Sum.
Elementarpartiklarna som bygger universum har två typer:bosoner och fermioner, där fermionerna klassificeras som Dirac, Weyl, och Majorana fermioner. Under de senaste åren har Weylfermioner finns i system med kondenserat material, och Weyl-halvmetaller som en slags kvasipartikel, och de manifesterar sig som Weyl pekar från spridningsförhållanden. I motsats till högenergifysik som kräver den stringenta Lorentz-symmetrin, det finns två typer av Weyl-punkter i system med kondenserat material:Weyl-punkter av typ I med symmetriska konliknande bandstrukturer och Weyl-punkter av typ II med kraftigt lutande bandstrukturer.
Typ II Weyl-punkter har observerats i system med kondenserad materia och flera konstgjorda periodiska strukturer, såsom fotoniska och fononiska kristaller. Dock, dessa Weyl-punkter av typ II är inte symmetrirelaterade, och de har små separationer och olika energier. Således, det är utmanande att särskilja typ II Weyl-punkterna med andra degenererade punkter och observera relaterade fenomen som topologiska yttillstånd.
Nyligen, Dr Rujiang Li och professor Hongsheng Chen från Zhejiang University, Dr. Bo Lv och Prof. Jinhui Shi från Harbin Engineering University, Prof. Huibin Tao från Xi'an Jiaotong University, och Prof. Baile Zhang och Prof. Yidong Chong från Nanyang Technological University observerar de idealiska typ II Weyl-punkterna i klassiska kretsar genom att utnyttja den höga flexibiliteten hos kretsnodanslutningar. För en kretsstruktur med periodiska gränser i tre dimensioner (Fig. 1a), detta Weyl-system har bara två band. På grund av skydden från spegelsymmetrier och tidsreverseringssymmetri, det finns det minimala antalet fyra typ II Weyl-punkter i momentumrymden och dessa Weyl-punkter ligger på samma frekvens. Experimentellt, de bevisar förekomsten av linjära degenererade punkter och den starkt lutande bandstrukturen genom att rekonstruera bandstrukturerna i kretssystemet (fig. 1b-c), vilket innebär att dessa fyra Weyl-punkter är idealiska Weyl-punkter av typ II. Förutom, de tillverkar en kretsstruktur med en öppen gräns (Fig. Id) och observerar de topologiska yttillstånden inom ett ofullständigt bandgap (Fig. 1e-f). Dessa fenomen innebär vidare att det finns idealiska Weyl-punkter av typ II.
Kretssystem har hög flexibilitet och kontrollerbarhet. Jämfört med andra experimentella plattformar, gitterplatser i ett kretssystem kan kopplas på ett godtyckligt sätt med godtyckliga antal anslutningar per nod och långdistansanslutningar, och hoppstyrkorna är oberoende av avståndet mellan noderna. Just på grund av denna flexibla och mycket anpassningsbara anslutning, och avståndsoberoende hopp, ett kretsgitter som kan observera de idealiska typ II Weyl-punkterna är lätt att tillverka. Denna kretsplattform kan användas för vidare studier av Weyls fysik och andra topologiska fenomen.