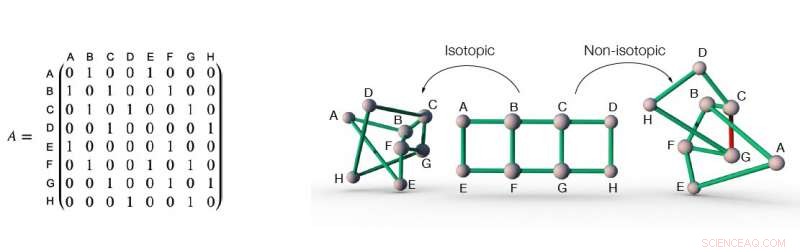
Närliggande matris för ett nätverk (vänster), och tre olika inbäddningar av detta nätverk i rymden (höger). Nätverkets närliggande matris registrerar information om nätverkets anslutning. Till exempel, i nätverket i figuren, nod A och B är sammankopplade med en länk, därför är elementet i närliggande matris vid skärningspunkten mellan rad A och kolumn B ett. Liknande, nod A och C är inte sammankopplade med en länk, därför är elementet i närliggande matris i skärningspunkten mellan rad A och kolumn C noll. De två första nätverksinbäddningarna av nätverket som beskrivs av närliggande matris till vänster är isotopiska till varandra, eftersom de kan omvandlas till varandra genom att helt enkelt "platta ut" inbäddningen, utan att behöva klippa upp någon länk. Å andra sidan, inbäddningen till höger är icke-isotop till de andra två inbäddningarna, för att förvandla det till de andra två, minst en länk (den röda länken till exempel) måste skäras upp för att låta andra länk(ar) passera. Kredit:Liu, Dehmamy &Barabási.
Strukturen och funktionerna hos många fysiska nätverk, inklusive den mänskliga hjärnan, kärlsystemet och andra biologiska nätverk, beror ofta på deras tredimensionella och geometriska layout. Att skilja mellan fysiska nätverk med identiska anslutningar men olika geometriska layouter, dock, kan vara mycket utmanande.
Forskare vid Northeastern University har nyligen introducerat en teoretisk konstruktion som kallas nätverksisotopi som kan hjälpa forskare att skilja mellan fysiska nätverk. Nätverksisotopi erbjuder ett klassificeringsverktyg som beskriver klasser av 3D-nätverkslayouter som kan omvandlas till varandra utan länkkorsningar.
"Vårt projekt började som en nyfikenhet på nätverkslayouter, "Yanchen Liu, en av forskarna som genomförde studien, berättade för Phys.org. "Det finns många 3-D-printade nätverk på vårt kontor som studerats i olika projekt i labbet. När man tittar på dessa nätverk, vi undrade:Om det för ett givet nätverk (fast ledning av länkarna) finns oändliga sätt att placera noderna och länkarna i 3D-rymden, hur kan vi avgöra om två layouter i samma nätverk är lika eller olika? Dessutom, hur ska vi definiera likheterna mellan nätverkslayouter och om två layouter är olika, hur ska vi mäta skillnaden mellan dem?"
Kort efter att de började bedriva sin forskning, Liu och hennes kollegor insåg att det finns två huvudsakliga sätt på vilka nätverksgeometriska layouter kan skilja sig från varandra. Den första av dessa beror på i vilken utsträckning ett nätverks layout är utsträckt, medan den andra är resultatet av så kallad länkkorsning (dvs. länkar som går genom varandra).
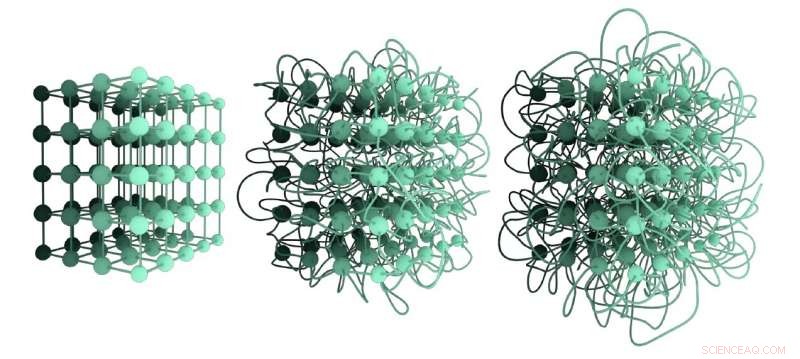
Tre olika icke-isotopiska inbäddningar av samma gitternätverk. Inbäddningen till vänster är otrasslad; inbäddningen i mitten är mer trasslig jämfört med den första, och den tredje inbäddningen är den mest trassliga. Deras nivå av trasslighet kan kvantifieras med graflänkningsnumret. Kredit:Liu, Dehmamy &Barabási.
"Den första typen av skillnad är trivial, men den andra typen av skillnad är spännande, " Liu förklarade. "Liknande frågor har studerats i knutteorin, vilket är ett fält dedikerat till knutar som bildas av en eller flera slutna kurvor."
Ett fysiskt nätverks inbäddning (dvs. layout) är i huvudsak en beskrivning av hur dess noder och länkar sätts ihop i rymden. I deras papper, Liu och hennes kollegor introducerade ett koncept som kallas nätverksinbäddningsisotopi som kan användas för att skilja mellan olika möjliga inbäddningar av ett givet nätverk i 3D-rymden.
"Om två nätverksinbäddningar är isotopiska för varandra, det betyder att de kan sträckas in i varandra utan att behöva skära upp någon länk för att låta andra länkar passera, " sa Liu. "Å andra sidan, om två nätverksinbäddningar är icke-isotopa för varandra, det betyder att de aldrig kan omvandlas kontinuerligt till varandra utan att skära av länkar."
Begreppet nätverksisotopi, som det definieras av detta team av forskare, kan användas för att mäta i vilken utsträckning olika nätverksinbäddningar är trassliga, ett mått som kallas grafens länknummer. Intressant, Liu och hennes kollegor fann att detta mått också är korrelerat med en layouts elastiska energi.
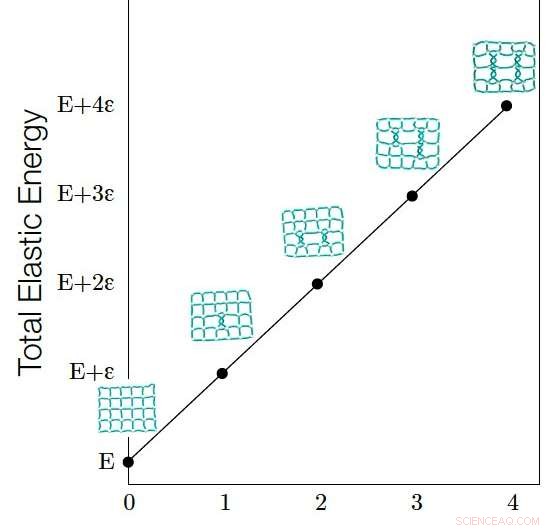
Den elastiska energin (E) hos en nätverksinbäddning observeras vara linjärt korrelerad till dess graflänkningsnummer (G). Den elastiska energin hos en nätverksinbäddning är proportionell mot den totala längden av alla länkar. Den linjära relationen mellan E och G kan förklaras av det faktum att varje ökning av G sträcker ut länkarna i nätverksinbäddningen, vilket i sin tur ökar E, och mängden energiökning som orsakas av varje härva (varje härva får G att öka med en) är kvantiserad och en konstant. Kredit:Liu, Dehmamy &Barabási.
Många fysiska system kan beskrivas som nätverk, en betydande del av dem är fysiska nätverk. De teoretiska begrepp som introducerats av forskarna är effektiva verktyg för att studera egenskaperna och geometriska egenskaperna hos dessa system.
"Det finns tre viktiga landvinningar i detta dokument, enligt min åsikt, " sa Liu. "Den första är att vi definierade nätverksinbäddningsisotopi, som är en förlängning av knutisotopi från knutteori till nätverksinbäddningar. Det andra är att vi uppfann grafens länknummer, ett användbart mått på graden av trasslighet av nätverksinbäddningar. Till sist, fann vi att grafen som länkar numret för en nätverksinbäddning är korrelerad med den elastiska energin för den nätverksinbäddningen."
Liu och hennes kollegor använde sina rön för att utveckla en statistisk modell som beskriver bildandet av tovor i ett fysiskt nätverk. I framtiden, denna modell skulle kunna användas för att utvärdera i vilken utsträckning 3D-layouten av ett fysiskt system är trassligt.
I deras senaste tidning, till exempel, forskarna använde det för att undersöka trassligheten i många fysiska system, inklusive mushjärnan. Eftersom alla teoretiska konstruktioner som introduceras i denna artikel kan tillämpas på en mängd olika fysiska nätverk, de skulle i slutändan kunna stödja fysikforskning med fokus på ett brett spektrum av ämnen.
"Vi fortsätter nu studien av fysiska nätverk, " sa Liu. "För närvarande, Jag arbetar på ett specifikt fysiskt nätverk:fruktflugans larvhjärnnätverk, vilket är ett nätverk som bildas av neuroner inbäddade i 3D-rymden. Vi är särskilt intresserade av kopplingarna mellan det fysiska hos detta nätverk (dess inbäddning) och dess strukturella egenskaper (hur nervcellerna är anslutna genom neuronala ledningar).
© 2020 Science X Network