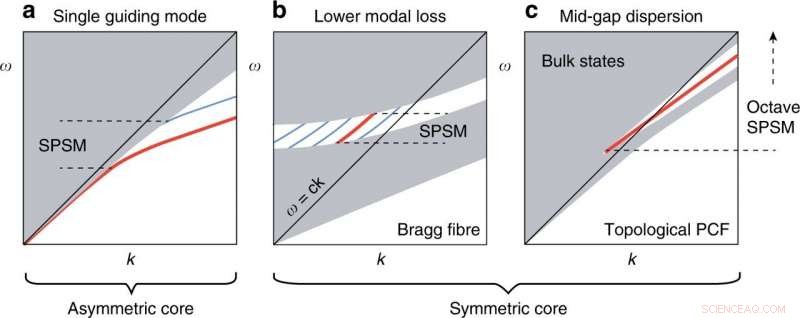
Asymmetriska och symmetriska förhållningssätt till en SPSM. (a) Dominant tillvägagångssätt för att dela upp de degenererade fundamentala lägena genom strukturell asymmetri. (b) Föreslagen Bragg-fiberdesign för att styra ljus genom ett enskilt degenererat läge med lägre förlust än andra lägen. (c) Den topologiska PCF tillhandahåller singlett mid-gap-dispersion för ett bredbands-SPSM. Kredit:Light:Science &Applications, doi:10.1038/s41377-020-00432-2
Optiska fibrer gjorda av topologiska fotoniska kristaller möjliggör förbättrad mångsidighet och kontroll över de lägen och polarisering av ljus de sänder. Kompositionsmässigt, fotoniska kristaller innehåller bandgap för att förhindra passage av ljus i förhållande till specifika vågenergier och momenta ungefär som en på/av-knapp. I en ny rapport som nu publiceras den Nature Light:Science &Applications , Hao Lin, och Ling Lu vid Institutet för fysik vid den kinesiska vetenskapsakademin sände rent "single mode"-ljus över ett stort frekvensområde via en topologisk egenskap känd som en "Dirac-virvel". Konceptet kan leda till applikationer som överför ljussignaler mer stabilt över långa avstånd. Även om arbetet för närvarande är teoretiskt, forskarna föreslår användning av fibrer gjorda av kiseldioxid baserade på stapla-och-drag-metoder eller tredimensionella (3-D) utskriftstekniker för att tillverka och testa dessa teoretiska koncept.
Förstå knutlinjerna och Weyl -punkterna i en fotonisk kristallfiber.
Fotoniska kristallfibrer förlitar sig på den oändliga mängden tvådimensionella (2-D) kristaller för sin funktionalitet. Konceptet med topologisk fotonik baserad på robusta vågledare kan inspirera till nya fiberkoncept inklusive utvecklingen av en envägsfiber inuti en magnetisk, 3-D fotonisk kristall. I det här arbetet, Lin och Lu introducerade en topologisk fotonisk kristallfiber (PCF) som liknar Dirac-virvelns topologiska hålighet i dess tvärsnitt med hjälp av 2-D fotoniska kristaller. Dirac vortexfibern är en idealisk design för att utveckla ultrabredbandssingelpolarisationssingelmode (SPSM) fibrer på grund av singel-midgap-spridningen inom bandgapet. Forskarna underlättade tillverkningssteget genom att introducera en förenklad design av endast fyra kapillärkiselrör för att slutligen uppnå en oktavspännande SPSM.
Teamet började med den vanligaste fotoniska kristallfibern, en fotonisk kiselkristall med ett triangulärt gitter av lufthål. Materialet innehöll två nodallinjer av 2-D Dirac-punkter i Brillouin-zonen. Om de bröt inversionssymmetrin hos den fotoniska kristallfibern genom att lägga till ett extra litet lufthål i den primitiva cellen, varje nodlinje i konstruktionen kan spalta in i Weyl-punkter eller topologiska laddningar på materialet. Weyl-partiklar är svårfångade fermioniska partiklar med försvinnande massa och finns inte som en elementarpartikel i naturen. De visar sig istället dyka upp i fasta material där 3D-band kan utveckla en topologiskt skyddad punktliknande korsning, känd som en Weyl-punkt. Fotoniska Weyl-punkter kan realiseras i 3-D fotoniska kristaller med komplexa strukturer.
Banddiagram av kiseldioxid (ε = 2,1) fotoniska kristallgitter enhetliga i riktning utanför planet (z). (a) Projicerat banddiagram för den triangulära fotoniska kristallen, där nodal-line degenerationen markeras. (b) Ett extra lufthål i den primitiva cellen bryter inversionssymmetrin, och nodlinjen lyfts till Weyl-punkter. Insättningar:tvärsnittsstrukturer och bandstrukturer i planet vid kza/2π = 2,02. Två olika primitiva cellval ritas i (a). Kredit:Light:Science &Applications, doi:10.1038/s41377-020-00432-2 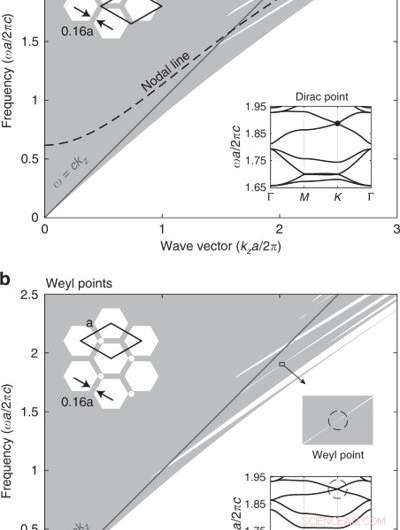
Det topologiskt bundna tillståndet som undersöks i detta arbete kan också realiseras i bikakegitter med alternerande enkel- och dubbelbindningsrepresentationer av organiska föreningar som kallas Kekulé-strukturer, uppkallad efter den tyske kemisten August Kekulé, som ursprungligen föreslog representationen att utveckla den organiska bensenföreningen. Forskarna kopplade sedan ihop de två nodallinjerna av Dirac-punkter i en förstorad supercell och förinlade dem till ett bandgap. Varje supercell hade tre primitiva celler märkta som en konstgjord "atom" innehållande tre strävor. De flyttade varje atom i strukturen genom att flytta dess masscentrum i valfri riktning genom att justera tjockleken på de tre strävorna utan att ändra atomens totala massa. Forskarna utvecklade Kekulé-moduleringar av gittren och ritade deras motsvarande bandstruktur.
Stabiliteten hos den fotoniska kristallfibern i Dirac vortex förblev i själva designen eftersom motsvarande topologiska defekt inte bildades genom att lägga till eller ta bort material lokalt. Den topologiska defekten bildades genom att försiktigt störa hela gittret för att skapa små lokala defekter. En avgörande topologisk egenskap hos Dirac-virvelfibern var lättheten att skapa flera nästan degenererade lägen genom att öka lindningstalet – dvs ett heltal som representerar antalet gånger som kurvorna rör sig moturs runt en punkt, av virveln. I princip, forskarna kan praktiskt taget tillverka en kontinuerlig, single-mode eller multimode Dirac vortex fotonisk kristallfiber antingen från 3D-tryckta förformar (en form eller form), eller via stack-and-draw-metoden som används för att utveckla optiska fibrer med mer än hundra rör med olika rörtjocklekar. Dock, ingen av dessa metoder var bekväma, därför Lin och Lu et al. presenterade en diskret version av fiberdesign.
Dirac-virvelfiber erhållen genom kontinuerliga Kekulé-moduleringar. (a) Exempel på hur en "atom" kan förskjutas i vilken riktning som helst (arg[δ] = ϕ) med ändlig amplitud (|δ|) genom att ändra bredden på de tre strävorna. (b1), (c1), (d1) Supercellexempel på tre koordinerade atomer (A1, A2, och A3). Motsvarande bandstrukturer plottas i (b2), (c2), och (d2), respektive. (e) Struktur av en kontinuerlig Dirac-virvel PCF, där varje sträva är färgad efter dess bredd. (f) Banddiagram för fibern avsatt med hänvisning till frekvensen för den ursprungliga nodlinjen (den centrala streckade linjen). Insättningen visar intensitetsmönstren för det topologiska läget och ett läge med lokal defekt. Enkeltpolariseringens topologiska läge (röd linje) sträcker sig över två oktaver. Kredit:Light:Science &Applications, doi:10.1038/s41377-020-00432-2 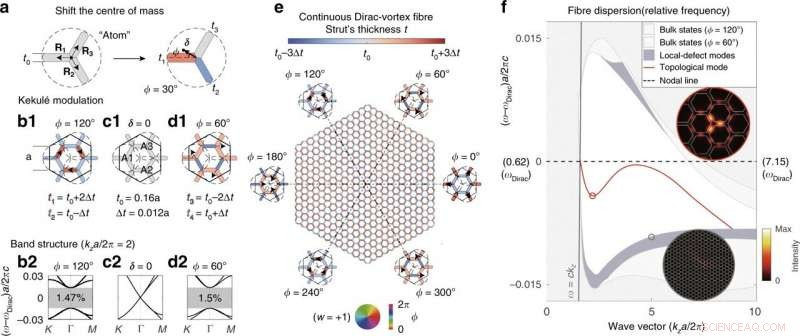
Forskarna krävde bara fyra rör för att stapla och rita Dirac vortex fotoniska kristallfiber, vilket var mycket rimligt att tillverka. De fyra kiseldioxidrören som användes i processen hade samma ytterdiameter för att bibehålla gallret, men olika inre diametrar för modulering. Forskarna plottade den resulterande diskreta Dirac-virvelfibern och dess bundna struktur där strukturell olikformighet var närvarande vid sex identiska gränssnitt. De noterade också närvaron av indexstyrda lägen i Dirac-virvelfibern som inträffade varhelst ett skarpt lokalt maximum av strävans tjocklek fanns. Dessa motsvarade en lokal ökning av det effektiva brytningsindexet. Forskarna noterade också fibertvärsnittet med virvelstorleken och motsvarande bandstruktur.
Dirac vortex fotoniska kristallfiber med en ändlig virveldiameter upprätthöll ett enkelpolariseringssingelmod (SPSM). Lin och Lu et al. testade deras potentiella prestanda i förhållande till förlusten av förlossningen, dispersion och effektiv area och böjförlust. De ritade in lägena med den lägsta inneslutningsförlusten och noterade att förlusten av det topologiska läget var den lägsta för hela våglängdsområdet över en oktav. Specifikationerna för Dirac vortex fotoniska kristallfiber som beskrivs här liknade de i tidigare studier, även om med nyckelskillnaden i ett enkelpolariseringsläge, används i detta arbete.
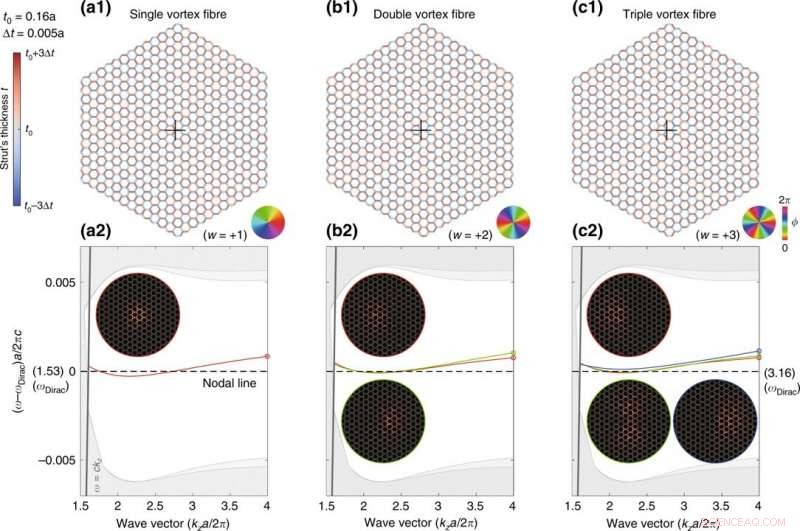
Kontinuerliga Dirac-virvelfibrer med lindningsnummer w = +1, +2, +3. (a1), (b1), och (cl) är fiberstrukturerna. Färghjulen visar motsvarande faser av den generaliserade Kekulé-moduleringen. (a2), (b2), och (c2) är motsvarande banddiagram, och infällningarna visar lägesprofilerna (zˆ⋅Re[E∗×H]) för lägen vid kza/2π = 4. Kredit:Light:Science &Applications, doi:10.1038/s41377-020-00432-2
Octave SPSM i en kontinuerlig Dirac-virvelfiber med en ändlig virvelstorlek. (a) Fiberstruktur med 16 kapslingsperioder i radie. Färghjulet representerar fasen och amplituden för den generaliserade Kekulé-modulationen. (b) Fullständig fiberspridning i absolut frekvens. Första topologiska läge (röd linje) och högre ordningens dubblettlägen (grön prickad linje) i det första topologiska bandgapet, samt ett andra topologiskt läge (blå linje) i det andra topologiska bandgapet vid högre frekvens. Modprofilerna (zˆ⋅Re[E∗×H]) för de två topologiska lägena visas i insättningarna, inringad med olika färger för tydlighetens skull. (c) Fiberdispersion i frekvens i förhållande till den ursprungliga nodal-line-frekvensen. (d) Instängningsförluster för de guidade lägena. (e) Dispersionsparameter och effektivt område i det första topologiska läget. (f) Böjförlust av den första topologiska moden vid λ = 1550 nm. Kredit:Light:Science &Applications, doi:10.1038/s41377-020-00432-2 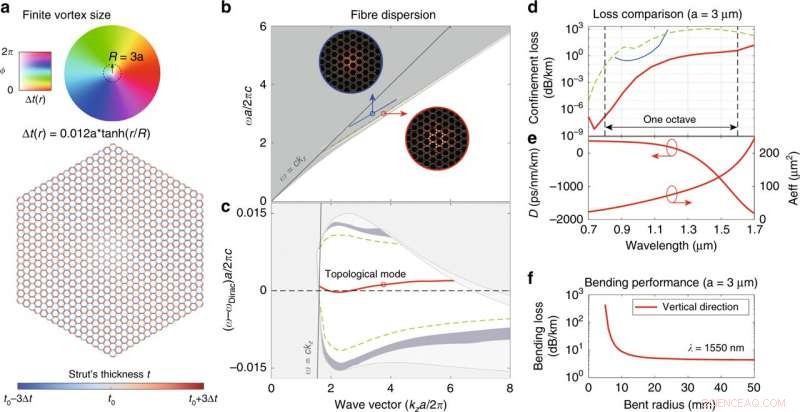
På det här sättet, Hao Lin och Ling Lu undersökte numeriskt Dirac vortex-topologiska fotoniska kristallfiber i förhållande till dess princip, konstruktion och potentiell prestanda. De föreslog att utveckla denna fiber med den vanliga stapel-och-drag-processen med hjälp av kiseldioxidglasrör eller 3D-tryckta förformar. Metoden är fördelaktig jämfört med tidigare fibrer på grund av dess förmåga att styra valfritt antal nästan degenererade lägen efter behag. Singelmodsdesignen gav enkelpolariseringen, singelmodsfiber med en oktavbandbredd för att enkelt ställa in det effektiva lägesområdet genom att ändra virvelstorleken i materialet. Arbetet föreslår att fotoniska kristallfibrer används som en ny plattform för topologisk fotonik.
© 2020 Science X Network