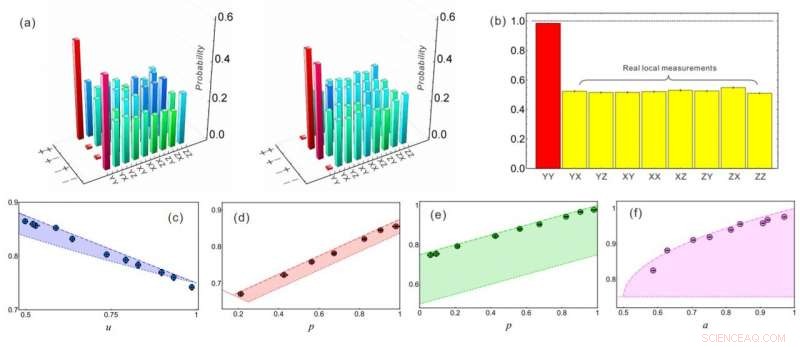
Experimentella resultat för lokal statlig diskriminering. Kredit:WU Kangda et al.
Nyligen, ett forskarlag ledd av akademikern Guo Guangcan från CAS Key Laboratory of Quantum Information vid University of Science and Technology of China (USTC) i CAS, har gjort viktiga framsteg inom kvantinformationsteorin. Prof. Li Chuanfeng och professor Xiang Guoyong från teamet samarbetade med Dr. Strelstov från University of Warszawa för att undersöka den imaginära delen av kvantteorin som en resurs, och flera viktiga resultat har erhållits. Relevanta resultat publiceras nu gemensamt som redaktörsförslag i Fysiska granskningsbrev och Fysisk granskning A .
Ett komplext tal är ett matematiskt verktyg, och det används ofta inom mekanik, elektrodynamik, optik och andra relaterade fysikområden för att ge en elegant formulering av motsvarande teori. Kvantmekanikens födelse ger en enhetlig bild av våg och partikel, och ytterligare stärker komplexa tals framträdande roll i fysiken. Dock, frågan om huruvida komplexa strukturer är nödvändiga för kvantmekaniken har länge diskuterats av fysiker
Forskare har betraktat det komplexa talet som en sorts kvantresurs, och avslöjar dess oersättliga roll i den lokala diskrimineringen av tvådelade kvanttillstånd. Vidare, inom ramen för kvantresursteorin, de studerade mätmetoden för denna resurs och omvandlingsproblemet under olika fria operationer. De har löst problemet med robusthetsmätning av komplex storlek, transformation av enbits kvanttillstånd under fri drift, och sannolikhet för ömsesidig omvandling av något rent tillstånd under fri drift.
Genom att använda det intrasslade tillståndet med två fotoner som förbereds genom parametrisk nedkonvertering, forskare mätte och jämförde vidare framgångssannolikheten för lokalt särskiljande kvanttillstånd när de endast använde den verkliga mätgrunden och den allmänna mätgrunden. De observerade framgångsrikt ökningen av framgångssannolikheten när de använde den komplexa mätningsbasen, som verifierade komplexets viktiga roll i kvantmekaniken.
Detta arbete bevisar att den imaginära delen är oumbärlig i teorin om kvantmekanik. Recensenten rekommenderade det varmt, noterar "Jag tycker att kvantimaginariteten kan betraktas som en starkare form av kvantkoherens... Jag tror också att resultaten i manuskriptet kommer att stimulera forskning om kvantfundamentet och kvantresursteorierna med en rikare struktur."