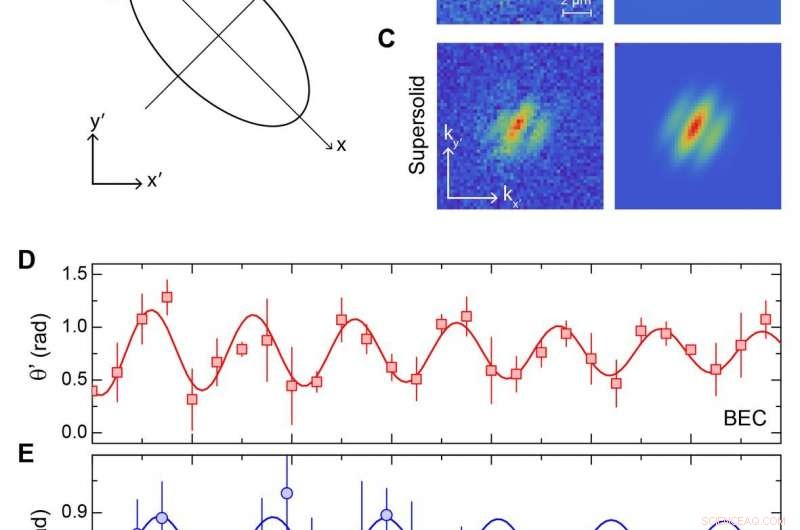
Saxlägesmått. A) Skiss av den experimentella geometrin:atomsystemet (ellips) är fångat i en anisotrop potential med egenaxlarna x och y. En plötslig rotation av infångningspotentialen exciterar en vinkeloscillation θ(t) (röda pilar). B-C) Exempel på de experimentella fördelningarna efter fri expansion och på motsvarande tvådimensionella passningar som används för att extrahera oscillationsvinkeln θ 0 efter den fria expansionen i B) BEC-regimen (dd=1,14); C) supersolid regim (dd=1,45). D-E). Tidsutveckling av vinkeln θ 0 (t):D) BEC-regim; E) supersolid regim. Felstaplar representerar standardavvikelsen för 4-8 mätningar. Kredit:Vetenskap, doi:10.1126/science.aba4309
Superfluiditet i vätskor och gaser kan visa sig som ett minskat tröghetsmoment (massans rotationsanalog) under långsamma rotationer. Icke-klassiska rotationseffekter kan också övervägas i de svårfångade supersolida faserna av materia där superfluiditet kan samexistera med en gitterstruktur. I en ny rapport som nu publiceras i Vetenskap , L. Tanzi och en forskargrupp vid National Institute of Optics och Institutionen för astronomi vid universitetet i Florens i Italien, visade hur en nyligen upptäckt supersolid fas i dipolära kvantgaser hade ett minskat tröghetsmoment. Teamet studerade ett märkligt rotationsoscillationsläge i en harmonisk potential för att härleda en supersolid fraktion och ge direkta bevis på den supersolida naturen hos den dipolära konstruktionen.
Superfluids och supersoliditet
Superfluids uppvisar sina mest spektakulära egenskaper under rotation, där det superfluidiska tillståndet beskrivs av en makroskopisk vågfunktion. Fysiker hade redan verifierat icke-klassiska rotationseffekter för de flesta kända supervätskor inklusive kärnämne, gasformiga Bose-Einstein kondenserar och degenererar Fermi-gaser. Resultatet är relaterat till Meissner-effekten noterad i supraledare. På 1960-talet forskare upptäckte en annan typ av bosonisk fas av materia känd som ett supersolid, beskrivs av en makroskopisk vågfunktion. I en supersolid, superfluiditet kan samexistera med en arkitektur av kristalltyp. Fysikern föreslog att den roterande supersoliden skulle visa ett tröghetsmoment mellan ett superfluid och ett klassiskt system. Detta fenomen är känt som den icke-klassiska rotationströgheten (NCRI). Dessa observationer om supersoliditet gjordes främst med hjälp av fast helium, där forskare använde torsionsoscillatorer (rotationssystem) för att detektera NCRI. I det här arbetet, Tanzi et al. undersökte en annan supersolidkandidat – ett gasformigt Bose-Einstein-kondensat (BEC) av starkt dipolära atomer.
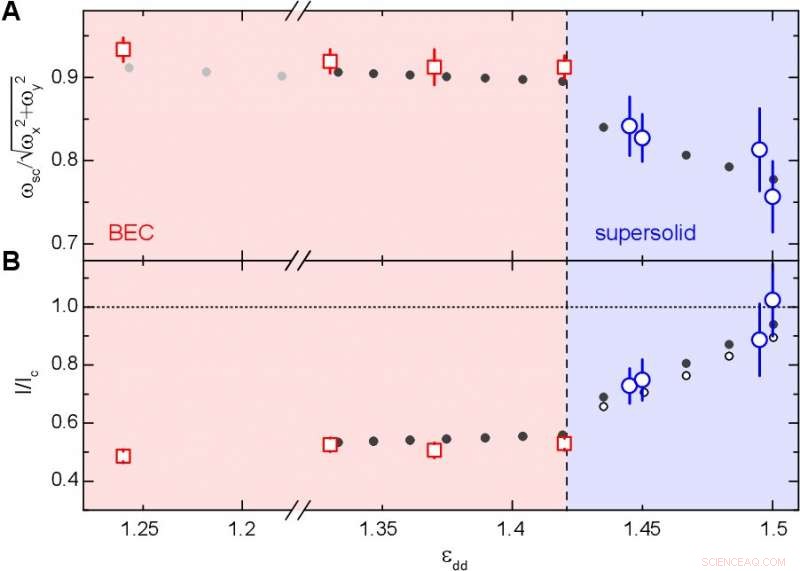
Saxläges frekvens och tröghetsmoment kontra interaktionsparametern. A) Frekvenser i saxläge. Stora cirklar och fyrkanter är de experimentella måtten. Svarta diamanter och prickar är de teoretiska förutsägelserna för medelfältet och bortom medelfältet, respektive. B) Tröghetsmoment. Stora kvadrater och cirklar härleds från ekv. (1) i studien, använda de experimentella mätningarna av saxfrekvenserna och det teoretiska β; svarta prickar är den numeriska simuleringen. Små öppna punkter är den teoretiska förutsägelsen för β 2. Felstaplar är en standardavvikelse. Experimentet har en kalibreringsosäkerhet på 3 %. Den streckade linjen som skiljer BEC och supersolid regimer bestämdes numeriskt. Kredit:Vetenskap, doi:10.1126/science.aba4309
BEC bildas vid en bråkdel över absolut noll och endast i atomer som fungerar som bosoner, en av två typer av fundamentala partiklar. När bosonerna kyls till tillräckligt låga temperaturer, en betydande del går spontant in i ett enda kvanttillstånd i ett fenomen som kallas Bose-Einstein-kondensation (BEC), och de mest kända experimenten är de som involverar atomgaser. Det nyligen upptäckta kvantsystemet visade en densitetsmodulerad regim samexisterande med faskoherensen, som krävs för supersoliditet. Forskare hade testat den superfluidiska naturen med hjälp av icke-roterande excitationslägen i förhållande till hydrodynamiska ekvationer för superfluider. I enlighet med föregående heliumexperiment, Tanzi et al. fokuserade endast på att karakterisera NCRI (icke-klassisk rotationströghet) för system, för att ge direkt bevis på överfluiditet under rotation.
Experimenten
Inom kvantfysik, Det är fortfarande opraktiskt att uppnå dipolära fasta ämnen som är tillräckligt stora för att realisera en cylindrisk geometri. Som ett resultat, forskarna valde en specifik rotationsteknik för att passa den asymmetriska, litet system i labbet. De exciterade sedan systemets så kallade saxläge; en liten vinkel rotationsoscillation av den harmoniska potentialen som naturligt håller systemet. Tekniken användes tidigare för att påvisa superfluiditet i vanliga Bose-Einstein-kondensat (BEC). Tanzi et al. undersökte den förändrade frekvensen av saxläge över övergången från BEC till supersolidformen för att direkt jämföra supersolid med ett helt superfluid system. Under experimenten, laget använde en BEC av starkt magnetiska Dysprosium (Dy) atomer i en anisotrop harmonisk fälla med frekvenser med dipolerna orienterade i Z-riktningen via ett magnetfält. Systemets temperatur var tillräckligt låg och forskarna inducerade övergången från BEC till supersolid genom att trimma via en magnetisk Feshbach-resonans och van der Waals interaktionsenergier. Forskarna förväntade sig att gittret skulle bestå av ett kluster supersolid för att få systemet till en droppkristallregim utan koherens mellan dropparna.
Superfluid fraktion från BEC till supersolid. Röda fyrkanter och blå cirklar är den superfluidiska fraktionen från den experimentellt uppmätta saxfrekvensen och den teoretiska β, använder Eq. (3) härledd i studien. Svarta prickar är den överflytande fraktionen från den teoretiska frekvensen. Öppna trianglar är den övre gränsen för den endimensionella superfluidfraktionen från Ekv. 4 härledda i studien. Diamanter är den uppskattade superfluidfraktionen av oberoende droppar. Infälld:den grå regionen är integrationsregionen för ekv. 4 härledda i studien. Kredit:Vetenskap, doi:10.1126/science.aba4309 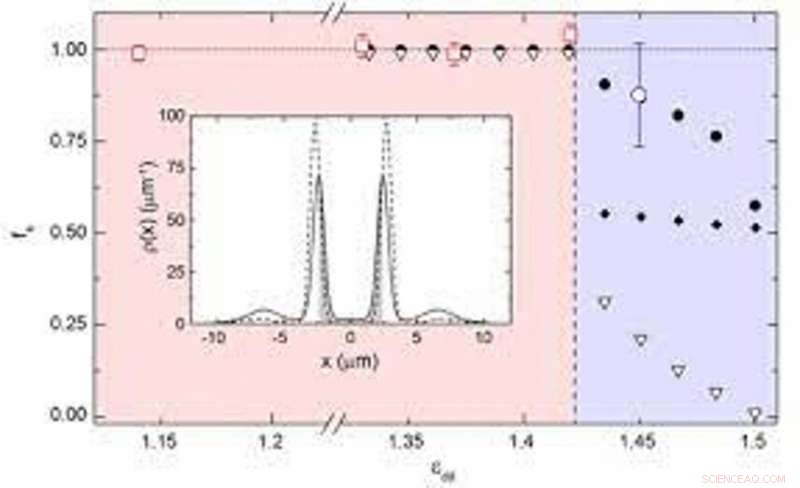
Teamet exciterade sedan saxläget och beräknade att oscillationsfrekvensen var direkt relaterad till tröghetsmomentet för supervätskan. De kopplade sedan tröghetsmomentet till en superfluidfraktion specifikt definierad för systemet. Tanzi et al. noterade analogin mellan saxläget och heliumtorsionsoscillatorerna eftersom båda systemen detekterade NCRI (icke-klassisk rotationströghet) via oscillationsfrekvensen. De experimentella resultaten sammanfattade saxmätningarna i BEC- och supersolid-regimerna. Teamet avbildade 2D-densitetsfördelningarna efter en fri expansion av systemet för att representera effektiva momentumfördelningar. BEC- och supersolid-regimerna visade enkelfrekvenssvängningar som förväntat för svagt interagerande supervätskor. För att undvika störningar orsakade av andra kollektiva lägen i systemet, Tanzi et al. använde två olika excitationstekniker för BEC- och supersolid-regimerna. De fick sedan en sammanfattning av resultaten för saxfrekvensen och det relaterade tröghetsmomentet och jämförde sedan resultaten med teoretiska förutsägelser. Teamet noterade en tydlig minskning av frekvensen när systemet gick in i supersolid-regimen i enlighet med teorin. Resultaten gav ytterligare bevis på NCRI för det dipolära fasta ämnet. Teamet förklarade mekanismerna som visas i detta arbete med hjälp av ursprungliga förutsägelser gjorda för Bose-kondensering i system med kondenserad materia.
Syn
På det här sättet, L. Tanzi och kollegor etablerade den superfluidiska naturen hos det dipolära supersolid genom att karakterisera dess icke-klassiska rotationströghet. Det superfasta materialet skilde sig från standardsuperfluider på grund av den reducerade superfluidfraktionen. Tekniken som beskrivs i detta arbete kommer att möjliggöra ytterligare undersökningar av fenomenen i framtida studier. Teamet föreslår att man uppnår större system som en ytterligare metod för att studera beteendet hos supersolider i ringformig geometri eller i en 2D-konfiguration, samtidigt som man studerar dynamiken hos kvantiserade virvlar i supersolidfasen.
© 2021 Science X Network