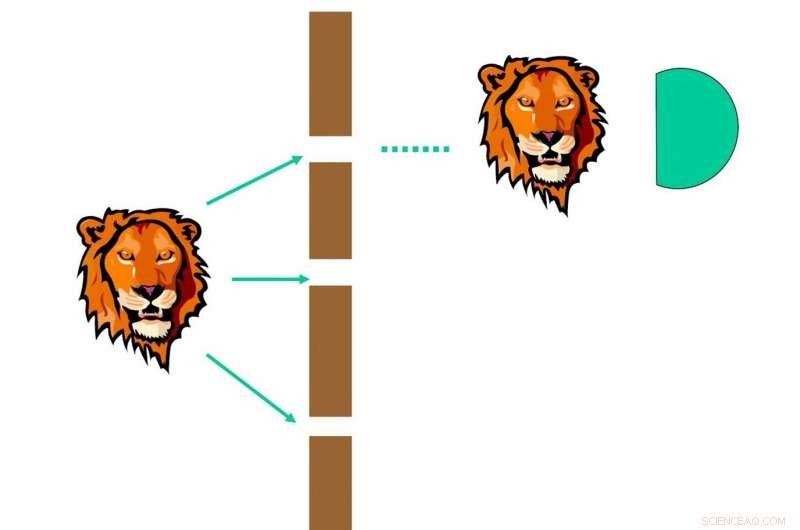
Kollaps i en delmätning. Hela vågfunktionen kollapsar till en egen stat som täcks av den uppmätta delvågfunktionen med viss sannolikhet, 1/3 i detta exempel. Upphovsman:Science China Press
Mätpostulatet är avgörande för kvantmekaniken. Om vi mäter ett kvantsystem, vi kan bara få ett av egenvärdena för den uppmätta observerbara, som position, energi och så vidare, med en sannolikhet. Omedelbart efter mätningen, systemet kommer att kollapsa till motsvarande egen stat omedelbart, känd som statskollaps. Det hävdas att den icke-klonande satsen faktiskt är ett resultat av mätpostulatet, eftersom icke-klonande teorem också skulle hålla i klassisk fysik. Möjligheten att klona i klassisk fysik är faktiskt förmågan att fullt ut mäta ett klassiskt system, så att ett klassiskt tillstånd kan mätas och förberedas.
För att tydligt förklara mätningen i kvantmekanik, det är bättre att använda följande exempel. Antag att en foton passerar genom en tre-identisk-slitsar och vi placerar en idealisk och icke-molekylär detektor efter varje slits. Enligt mätpostulatet, en av detektorerna kommer att upptäcka fotonen, och som ett resultat kommer hela vågfunktionen att kollapsa in i den slitsen.
Vad händer om vi bara placerar en enda detektor efter den övre slitsen? Det är naturligt att tro att det kommer att ha en tredjedel sannolikhet att upptäcka fotonen, och kollapsar hela vågfunktionen till slits-1, som visas i fig. 2. Men vad händer om detektorn vid den övre slitsen inte mäter fotonen? Detta är en delmätning. Detta påträffades i dualiteten quantum computing formalism, där linjär kombination av unitaries (LCU) föreslogs att utföra kvantberäkning.
Long föreslog att när man mäter en partiell våg, något kommer säkert att hända:(1) kollaps-in:det kommer att kollapsa till ett av egenvärdena med viss sannolikhet. Efter mätningen, hela vågfunktionen ändras direkt till motsvarande egenstat; (2) kollaps:den uppmätta vågfunktionen försvinner, och flytta till den omättade delen. Som visas i fig. 2, detektorn mäter fotonen med sannolikhet 1/3, och hela fotonvågfunktionen kollapsar in i den övre slitsen. Som visas i fig. 3 för kollaps, den uppmätta delen i den övre slitsen försvinner, och den omätade delen, nämligen vågfunktionen i mitt- och nedre slitsen ökar.
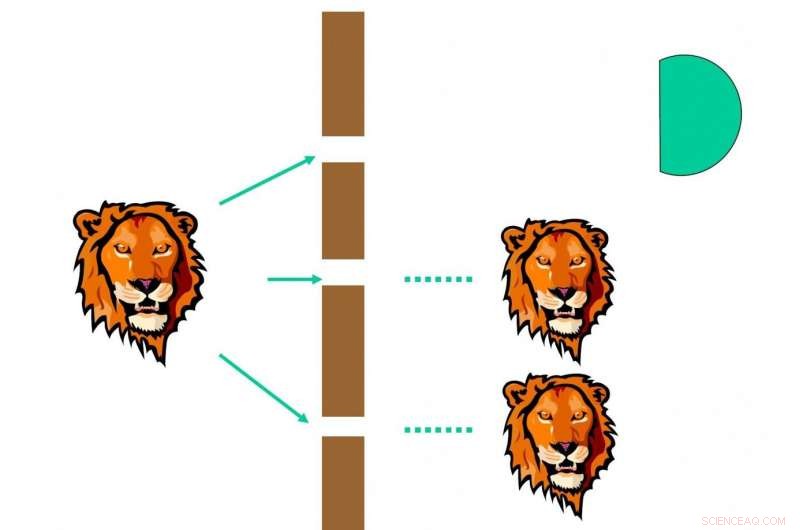
Collapse-out i en delmätning. Den uppmätta delen vid den övre slitsen försvinner, och den omätade delen vid mitten och låga slitsar ökas. Upphovsman:Science China Press
I verkligheten, delmätning är vanligare än fullmätning. Det bör noteras att kollaps-in och kollaps av partiella mätningar sker slumpmässigt inte bara i rymden, men också över tid. Till exempel, upptäckten av foton av en detektor kan naturligtvis förstås i termer av detta partiella mätningspostulat. När en fotons vågfunktion går till en detektor, det mäts inte fullt ut samtidigt, det är nämligen inte en fullständig mätning. Dess främre del kommer först till detektorn, träffar någon del av detektorn. Den faller antingen ihop vid någon punkt i det skärande området i detektorn eller kollapsar och motsvarande sannolikhet kommer att flyttas till en annan del av vågfunktionen. Denna process fortsätter tills fotonen detekteras. Om fotonen inte har detekterats förrän den sista delen av vågfunktionen når detektorn, då ökar amplituden för denna återstående vågfunktion till 1 för att med säkerhet detektera fotonen vid det sista steget.
Denna förklaring ges i uppfattningen att vågfunktion bara är kvantsystemet själv, WISE -tolkningen. I WISE -tolkning, det finns inget samband mellan vågfunktionen och kvantsystemet, vågfunktionen ÄR bara kvantsystemet. WISE -tolkningen stöds av mötet försenat val av experiment, som har rapporterats i olika medier för några år sedan.