s volym

I geometri är en oktagon en polygon med åtta sidor. En vanlig oktagon har åtta lika sidor och lika vinklar. Den regelbundna oktagonen är allmänt känd från stoppskyltar. En oktaedron är en åtta-sidig polyeder. En vanlig oktaedron har åtta trekanter med kanter av samma längd. Det är faktiskt två kvadratiska pyramider som möts vid sina baser.

Octagon Area Formula

Formeln för området med en vanlig oktagon med sidor av längden "a" är 2 (1 + sqrt (2 )) a ^ 2, där "sqrt" anger kvadratroten.

Derivation

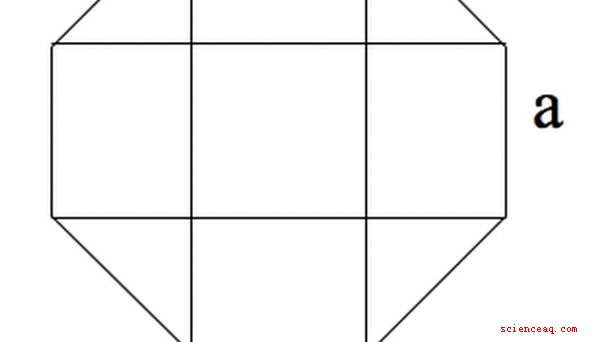
En oktagon kan ses som 4 rektanglar, en kvadrat i mitten och fyra isosceles trianglar i hörnen.

Torget är av område a ^ 2.

Trianglarna har sidor a, a /sqrt (2) och a /sqrt (2), enligt Pythagoras teorem. Därför har var och en ett område av ^ 2 /4.

Rektanglarna är av område a * a /sqrt (2).

Summan av dessa 9 områden är 2a ^ 2 ( 1 + sqrt (2)).

Octahedron Volume Formula

Formeln för volymen av en vanlig oktaedron av sidor "a" är en ^ 3 * sqrt (2) /3.

Derivation

Området med en fyrsidig pyramid är basenhet * höjd /3. Området med en vanlig oktagon är därför 2 * bas * höjd /3.

Base = a ^ 2 trivial.

Välj två intilliggande hörn, säg "F" och "C." "O" ligger i mitten. FOC är en isosceles rätt triangel med basen "a," så OC och OF har längd a /sqrt (2) av pythagorasatsen. Så höjd = a /sqrt (2).

Så volymen av en vanlig oktaedron är 2 * (a ^ 2) * a /sqrt (2) /3 = a ^ 3 * sqrt (2) /3.

Yta

Den vanliga oktaedans yta är ytan av en liksidig triangel av sidan "a" gånger 8 ansikten.

För att använda Pythagorasatsen, släpp en linje från toppen till basen. Detta skapar två rätt trianglar, med hypotenus med längden "a" och en sidlängd "a /2". Därför måste den tredje sidan vara sqrt [a ^ 2 - a ^ 2/4] = sqrt (3) a /2. Så är området för en liksidig triangel höjd * bas /2 = sqrt (3) a /2 * a /2 = sqrt (3) a ^ 2/4.

Med 8 sidor en vanlig oktaedron är 2 * sqrt (3) * a ^ 2.