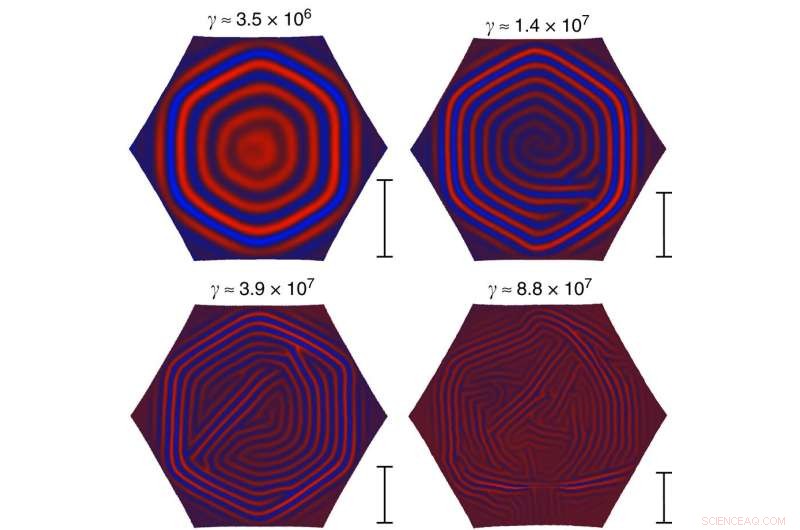
Skalning av domänstorlek. Typiska jämviktsrynkmönster i en sexkantig sektion av ett tunt sfäriskt skal på ett flytande substrat. Alla simuleringsparametrar hålls fasta, förutom plåttjockleken. Föppl–von Kármán-talet γ för systemet anges ovanför varje mönster. Medan det övre vänstra mönstret är tydligt uppdelat i sex domäner, verkar ökande γ minska den typiska domänstorleken. Skalstapeln till höger om varje mönster visar skalningen av typiska domänstorlekar som förutsägs av ekvation (20), upp till en konstant faktor (endast förhållandena mellan staplarna är meningsfulla eftersom ekvation (20) endast antyder skalningen av den typiska storleken och lämnar prefaktorn okänd). Kredit:Nature Communications (2017). DOI:10.1038/ncomms15809
Ett föremål som i sig är platt, säg ett papper, kan formas till en cylinder utan att sträcka eller riva det. Detsamma gäller dock inte för något som är krökt som en kontaktlins. När de komprimeras mellan två plana ytor eller läggs på vatten, kommer böjda föremål att platta till, men med rynkor som bildas när de bucklas.
Nu har forskning från University of Pennsylvania, University of Illinois Chicago (UIC) och Syracuse University visat att det med viss enkel geometri är möjligt att förutsäga mönstren för dessa rynkor, både var de kommer att bildas och i vissa fall deras riktning. Fynden, publicerade i Nature Physics , har en rad implikationer, från hur material interagerar med fukt och reflekterar solljus i naturen till hur en flexibel elektronik kan böjas.
"Det fina med det här arbetet är hur enkelt det verkligen är", säger Eleni Katifori, docent vid Penns institution för fysik och astronomi. "Det som ligger bakom är väldigt komplicerat, fysiken som översätts genom dessa regler har vi hittat, men själva reglerna är väldigt enkla. Det är inspirerande."
Meeting of minds
Sedan hennes doktorsexamen. har Katifori varit intresserad av mekaniken för hur tunna membran kröker. Även om detta förblev en kuriosa, vände hennes forskningsväg mot vätskeflödesnätverk istället. Sedan, medan hon samarbetade i ett projekt med Penn-kollegan Randall Kamien och sedan postdoktor Hillel Aharoni, observerade Katifori något hon inte kunde förklara vid den tiden. "Det vill säga, vi märkte att rynkorna bildades i domäner", säger hon.
Med andra ord, när en krökt yta blir tillplattad, slutar den med överflödigt material och efterföljande rynkor. Dessa rynkor dyker upp i mönster eller sektorer. "Frågan blev, varför ordnar sig rynkorna på det sättet?" säger Katifori. "Vi förstod inte hur viktiga domänerna i rynkningen verkligen är."
Vid en konferens 2016 hörde matematikern Ian Tobasco, biträdande professor vid UIC, Aharoni hålla ett föredrag om ämnet. "Det var första gången jag såg detta modellsystem presenteras", säger Tobasco. "Jag tyckte det var riktigt coolt." I mitten av 2017 publicerade Katifori, Aharoni och kollegor resultat om ämnet i Nature Communications , sedan vid en workshop senare samma år, träffade Tobasco Joseph Paulsen från Syracuse, som hade presenterat preliminära data om de experiment som hans grupp hade gjort på rynkor.
I början av 2018 började Tobasco arbeta på allvar med en matematisk teori för rynkor, och under lunchen på en konferens den sommaren kom Katifori, Tobasco och Paulsen överens om att de delade intresset för detta problem. De bestämde sig för att samarbeta, med fokus på att analysera hur mycket materialets fysiska form och krökningen från vilken det börjar kan ha betydelse för de skrynkliga mönstren.
Att lösa problemet
För vissa bakgrunder kan krökningen vara positiv, som rundheten hos en baseboll eller en jordglob, eller negativ, som en hästs sadel eller platsen på en glasflaska där halsen möter basen. Det finns också platt material, som ett papper.
I detta arbete fokuserade forskarna på positivt och negativt böjda skal.
Från varje tog de sedan bort grundläggande former, som trianglar, kvadrater och ovaler. "Tänk på en kakskärare. Låt oss säga att jag tar ett föremål med en positiv eller negativ krökning, sedan skär jag ut en av dessa former och lägger den på vätska", säger Katifori. Skulle det vara möjligt att gissa rynkmönstren och beräkna i vilken riktning rynkorna skulle flyta? För varje form skulle Tobasco lösa teorin baserat på de grundläggande principer han hade arbetat fram och publicerat på, och sedan komma med förutsägelser.
Baserat på dessa fynd genomförde Katifori och Penn postdoktorala forskare Desislava Todorova sedan simuleringar och matade in individuella former och parametrar i ett datorprogram. Liknande arbete hände i labbet som drevs av Paulsen, en biträdande professor i fysik vid Syracuse, genom experiment som han körde på polystyrenfilm 1 000 gånger tunnare än ett papper. "Den är gjord av samma material som att packa jordnötter", säger Tobasco, "men istället för den tredimensionella formen av en packningsjordnöt, tänk dig att den är platt som ett ark."
Genom simuleringar, experiment och mycket fram och tillbaka för att förfina processen och utöka den ursprungliga teorin, började trion urskilja att genom att tillämpa enkla geometriska principer kunde de i förväg veta vilket mönster rynkorna skulle ta och för en delmängd —vad de beskriver som "ordnade" rynkor—vilken riktning de skulle springa.
De geometriska principerna
För att förklara en sådan princip använder Katifori en femsidig polygon. "Först skriver jag in en cirkel i polygonen", säger hon. "Punkterna där den cirkeln rör vid polygonens kanter bestämmer var jag ritar mina linjer." Hon pausar för att skapa en andra form inuti den första, denna med fyra ojämna sidor; hon börjar varje linje där cirkeln och den yttre polygonen möts och förbinder alla fyra inre linjerna. "Nu har jag en, två, tre, fyra, fem domäner," fortsätter hon och pekar ut kvintetten av nyligen avspärrade sektioner.
För enkla former som denna kommer de yttre sektionerna att innehålla ordnade rynkor, som är organiserade och välordnade, enligt riktningen för de inre linjerna som Katifori ritade. Inom den nya inre polygonen bildas fortfarande rynkor, men de förblir oordnade och oförutsägbara.
Tobasco pekar på ett annat exempel, ett som han bestämde var universellt sant för former skurna från negativt böjda skal. "I slutändan är det väldigt enkelt att förutsäga rynkmönstren. Allt du behöver göra är att rita linjesegment som möter gränsen i rät vinkel." Med andra ord, börja vid en punkt i formen och skapa en direkt linje till formens kant, men bara på en plats där en rät vinkel sedan bildas.
Det tog ett år för laget att förstå. "Ekvationerna som bestämmer layouten på rynkor är fruktansvärda att lösa, och många av mönstren vi observerade i våra experiment och simuleringar är ganska komplicerade," säger Paulsen. "Men det visar sig att du under en viss uppsättning förhållanden kan förutsäga rynklayouten med en enkel uppsättning regler. Det betyder att vi nu har ett snabbt och effektivt sätt att designa rynkmönster."
"Dess enkelhet är vacker, och den är också användbar," tillägger han, särskilt för skrynkliga ytor som har en funktion som att möjliggöra vidhäftning eller vätskeflöde.
Katifori nämner liknande exempel. "Låt oss säga att det finns fukt eller fukt i luften. Vatten kommer att bete sig annorlunda i dalarna och kullarna på en räfflad yta", säger hon. "Genom att kontrollera rynkmönstret kanske du kan påverka hur vattnet kommer att kondensera."
Vad kommer härnäst
Forskarna har fortfarande mer att förstå om dessa komplexa texturerade ytor, som hur man drar mönster från oordnade rynkor, varför ordnade och oordnade domäner kan samexistera och varför det finns en "ömsesidighet" som länkar negativt och positivt böjda skal, vilket betyder att en gång mönstret för en är bestämd är det enkelt att förutsäga mönstret för den andra.
För nu säger de dock att de är exalterade över potentialen för vad de har lärt sig hittills.
"Du har en komplicerad teori som i slutet av dagen kokar ner till relativt enkel matematik som nästan alla kan göra med en kompass och en linjal", säger Katifori. "Det är en elegant och vacker lösning på ett komplext problem." + Utforska vidare