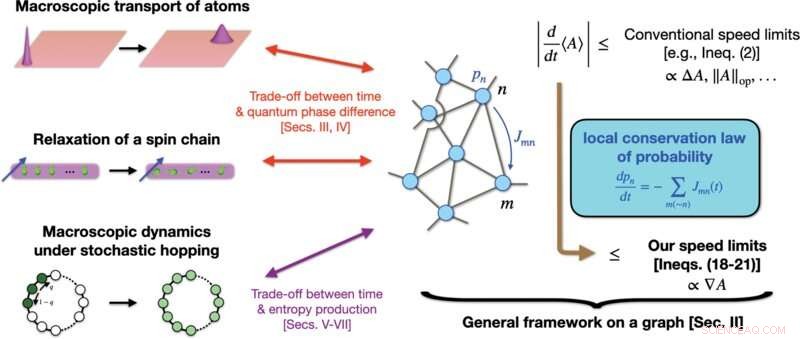
Schematisk illustration av våra prestationer. Vi upprättar ett allmänt ramverk för att härleda kvalitativt snävare hastighetsgränser av en kvantitet A än många konventionella, som beror på hela utbudet av A , såsom ΔA eller ∥A ∥op . Vår strategi är att kartlägga generell dynamik av vårt intresse till dynamik på en graf, där vi använder lokal bevarande av sannolikhet. Till skillnad från konventionella gränser innefattar våra hastighetsgränser gradienten ∇A av A på grafen, vilket avsevärt kan skärpa gränsen när ∇A ≪ΔA eller ∥A ∥op . När den tillämpas på makroskopiska kvantsystem (såsom makroskopisk transport av atomer eller relaxation av en lokalt störd spinnkedja), indikerar vår teori ett nytt kompromissförhållande mellan tid och kvantfasskillnaden. När den tillämpas på makroskopisk stokastisk dynamik, inklusive kvantdynamiken, indikerar vår teori ett avvägningsförhållande mellan tid och kvantiteter såsom entropiproduktionen. Kredit:PRX Quantum (2022). DOI:10.1103/PRXQuantum.3.020319
Ett uttryck för den maximala hastighet med vilken förändringar i makroskopiska system kan ske har härletts av en teoretisk fysiker vid RIKEN. Detta kommer att fördjupa vår förståelse av kvantfenomen i system som inte är i jämvikt.
En av de svåraste aspekterna av kvantmekaniken att förstå är Heisenbergs osäkerhetsprincip som säger att det inte är möjligt att samtidigt fastställa både position och momentum för ett objekt. Med andra ord, ju mer exakt en partikels position bestäms, desto bredare blir området för dess möjliga rörelsemängd (och vice versa).
1945 fokuserade två fysiker, Leonid Mandelstam och Igor Tamm, på en annan typ av osäkerhetsrelation, nämligen en mellan tid och energifluktuationer, och visade att övergångar i kvantsystem inte sker omedelbart; snarare begränsas hastigheten med vilken en övergång sker av en mängd som bestäms av hur mycket energin i systemet fluktuerar.
Många andra så kallade kvanthastighetsgränser har senare härletts, som har hjälpt till att bättre förstå kvantsystemens fysik och har varit användbara i olika kvanttillämpningar.
Men stora problem uppstår när kvanthastighetsgränser tillämpas på makroskopiska system. "Tidigare kvanthastighetsgränser, som är användbara för små system, blir vanligtvis meningslösa för makroskopiska övergångar", konstaterar Ryusuke Hamazaki från Nonequilibrium Quantum Statistical Mechanics RIKEN Hakubi Research Team. "Till exempel ger konventionella kvanthastighetsgränser en oändlig övre gräns för hastigheten på övergångar i en gas som består av atomer."
Nu har Hamazaki lyckats härleda en kvanthastighetsgräns för övergångar i makroskopiska system.
"Denna nya härledning ger grundläggande gränser som kan tillämpas på olika typer av kvantmakroskopiska fenomen utan jämvikt", säger han. "Jag hoppas att många grundläggande lagar och tillämpningar rörande makroskopisk kvantdynamik kommer att dyka upp baserat på de koncept som introduceras i denna studie."
Hamazaki härledde den strängare kvanthastighetsgränsen genom att utveckla ett allmänt ramverk baserat på sannolikhetslagens bevarandelag, en grundläggande princip inom fysiken.
Ett oväntat resultat för Hamazaki var upptäckten av en ny avvägningsrelation. "Istället för ett avvägningsförhållande mellan tid och energifluktuationer, som i Mandelstam-Tamm-gränsen, hittade jag ett mellan tid och gradienten för kvantfasen - en grundläggande storhet i kvantfysiken."
Hamazaki avser nu att utöka sin strategi för att se om den kan användas för att härleda kvanthastighetsgränser för kvantiteter som tillväxten av kvanttrassling. + Utforska vidare