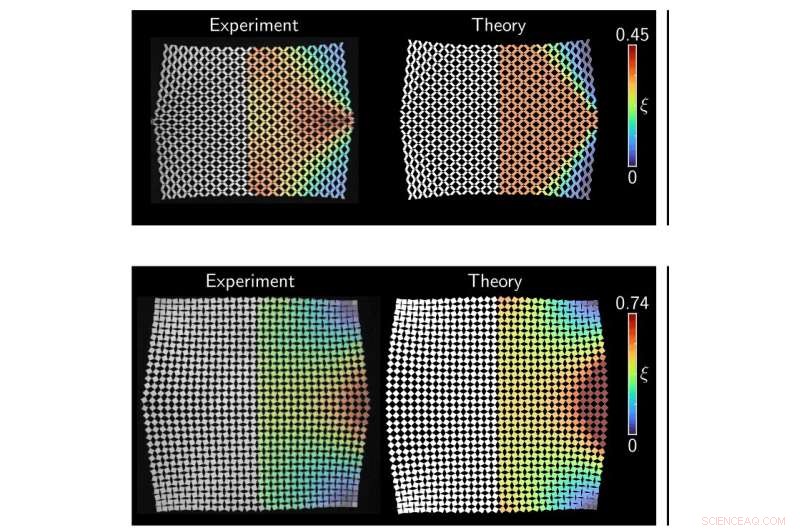
Två 16 × 16 cellmönster efter deformation. Den översta raden är nonauxetic (drar ihop sig när den dras) och hyperbolisk eller vågliknande. Nedre raden är auxetisk (expanderar när den dras) och elliptisk. Kredit:Paul Plucinsky
En traditionell papperskran är ett konstverk. Varje veck i origami leder till att ett enda fyrkantigt pappersark förvandlas till en fågel, en drake eller en blomma. Origami motverkar limning, markering eller skärning av papperet, men inom kirigamikonsten kan strategiskt placerade snitt förvandla papprets form ytterligare och skapa komplexa strukturer från enkla slitsar. Ett välkänt exempel på detta är en popup-bok, där beroende på hur det platta pappret är klippt, kommer en annan uppsättning former – ett hjärta, en groda, en uppsättning skyskrapor – att dyka upp när boken öppnas.
I tillverkningen förändrar kirigami spelet om vad som är möjligt. Precis som med papper, öppnar upprepad laserskärning av ett ark möjligheten för komplex formförändring som drivs av öppning och stängning av slitsar. På grund av den frihet som finns att utforma slitsar skapar detta ett brett urval av geometrier som har mycket anpassningsbara egenskaper jämfört med traditionella material. I verkliga applikationer kan du se ett sådant material som används i robotteknik eller rymden, till exempel ett ormskinn som kirigami-inspirerat material som gör att en robot kan krypa eller en flygplanskropp som förändras. Men innan dessa material kan anpassas för professionell användning, måste vi bättre förstå hur kirigami-material formskiftar under typiska tekniska påfrestningar och belastningar. Även om reglerna för enkla byggstenar är kända, är reglerna för deras kollektiva formskiftande interaktioner i stort sett oklara.
I en nyligen publicerad artikel publicerad i Physical Review Letters , ett tvärvetenskapligt team av forskare vid USC, University of Illinois i Chicago och Stony Brook University tog fram en ny matematisk ekvation för att kategorisera beteendet hos kirigami-inspirerade material för att bättre förutsäga hur de kommer att röra sig när de trycks eller dras. I teamet ingår USC Assistant Professor Paul Plucinsky och postdoktor Yue Zheng; Stony Brook University biträdande professor Paolo Celli och forskarassistent Imtiar Niloy; och University of Illinois-Chicago biträdande professor Ian Tobasco.
Plucinsky sa:"Geometrin hos dessa material är avstämd något godtyckligt. Så vi behöver regler om hur du kan välja de arkitekturer som du ska tillverka. När du väl har dessa regler måste du också kunna modellera systemet så att du gör en rimlig förutsägelse om hur den kommer att deformeras när den trycks eller dras."
Plucinsky säger att tidigare modeller av materialbeteende inte gäller kirigami-material, eftersom de inte är känsliga för den komplicerade geometrin i deras design. "Om du vill kunna använda dessa material måste du först förstå varför när du introducerar dessa mönster för laster, ger de ett mycket ojämnt svar."
När ett material skärs, producerar det "celler" eller inneslutna utrymmen som upprepas i ett mönster, till exempel parallellogram, sa Plucinsky. När det gäller kirigami-material kan dessa celler kategoriseras för att bete sig på ett av två sätt:vågliknande eller sönderfallande längs elliptiska bågar, och detta beror bara på om mönstret komprimeras eller expanderar vinkelrätt mot dragriktningen. En matematisk ekvation styr det geometriska beteendet hos saker som vattenflöde, sa Plucinsky, men för fasta ämnen som dessa är det svårare att härleda. En partiell differentialekvation (PDE) är vad Plucinsky och hans team kunde utveckla och lägga fram som den första biten i ett större pussel som krävs för att göra kirigami-material praktiskt användbara.
Ett modelleringsproblem
Just nu säger Plucinsky att även om människor är ivriga att använda kirigami-material för att designa enheter inom mjuk robotik, biomedicin och till och med rymdforskning, finns det ett grundläggande modelleringsproblem som förhindrar användningen av dem. Plucinsky sa att det inte finns mycket känt om hur kirigami-material fungerar under grundläggande belastningsförhållanden. "Om du inte har ett bra verktyg för att modellera systemen i fråga, skulle du ha svårt att undersöka designutrymmet och göra heltäckande förutsägelser om de individuella mönstren," sa Plucinsky.
I ljuset av det tänkte Plucinsky och hans forskargrupp, "finns det en enkel matematisk ekvation som skulle kunna karakterisera dessa material?" "Ekvationen," sa han, "skulle tillåta dig att förutsäga systemets beteende på ett numeriskt effektivt sätt ."
Nyckeln till ekvationen var att inse att kirigami-celler, även om de har komplicerade byggstenar i sig, kunde begreppsliggöras som atomer i ett gitter (en upprepande 2D-uppsättning av atomer), som i ett konventionellt kristallint fast ämne, där enheterna är identiska och upprepade . Därifrån var det enkelt att härleda en ekvation som lyckades återspegla förändringarna i den fysiska strukturen hos ett sådant material när det manipulerades. Ekvationen ger insikt i verkliga scenarier, till exempel hur ett kirigami-baserat rymdobjekt kan reagera om en månsten landar på det.
Pusslar designbitar
Kirigami-mönster, sa Plucinsky, är fördelaktiga av många skäl, varav en är att de är materialoberoende på många sätt. "Denna sorts paralleller är bra med additiv tillverkning där de nu i princip kan gå in och i olika skalor skapa noggrant konstruerade mönster. Poängen är att mönstret spelar roll, så om du designar mönstret rätt, gör valet av material du använder" det behöver inte spela lika stor roll."
Att se framgången med den matematiska modellen i att förutsäga kirigami-inspirerade material öppnar dörrarna för att använda sådan modellering för andra material, sa Plucinsky. "Vi arbetar mot idén att om du har något med ett upprepande mönster kan du hitta en ekvation som exakt modellerar det. Därifrån kan vi vända på det här så att om du vill konstruera en viss egenskap kan säga, 'åh, den måste ha ett x-typmönster' och bakåtkonstruera det." + Utforska vidare