
Detta är en ögonblicksbild tagen från en numerisk simulering av den tvådimensionella Wilson-Cowan-modellen med stokastisk input (Ekv. (3) i vår artikel). Gula (blå) pixlar representerar hög (låg) aktivitet. Kredit:Tiberi et al.
Tidigare neurovetenskaplig forskning tyder på att biologiska neurala nätverk i hjärnan kan självorganisera sig till ett kritiskt tillstånd. Inom fysiken är ett kritiskt tillstånd i huvudsak en punkt som markerar övergången mellan ordnade och oordnade faser av materia.
Forskare vid Jülich Research Centre, RWTH Aachen University och Sorbonne Université har nyligen introducerat en teori som kan hjälpa till att förklara kritikalitet i hjärnan. Denna teori, introducerad i en artikel publicerad i Physical Review Letters , är baserad på en prototypisk neurala fältteori, känd som den "stokastiska Wilson-Cowan-ekvationen."
"Tidigare arbeten har gett bevis för att hjärnan fungerar vid en kritisk punkt," sa Lorenzo Tiberi, Jonas Stapmanns, Tobias Kühn, Thomas Luu, David Dahmen och Moritz Helias, forskarna som utförde studien, till Phys.org, via e-post . "Ändå är det oklart vilken av de många möjliga typerna av kritik som är specifikt implementerad av hjärnan, och hur den senare kan utnyttja kritikalitet för optimal beräkning."
För att klassificera de olika typerna av kritik använder fysiker vanligtvis metoder inom den så kallade renormaliseringsgruppen (RG). Dessa är i huvudsak formella tillvägagångssätt som kan användas för att systematiskt undersöka förändringar i ett fysiskt system i olika skalor.
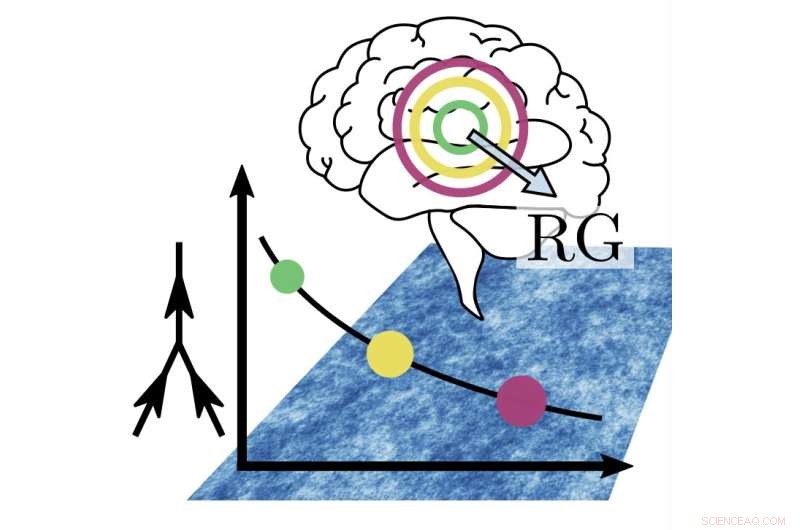
Abstrakt figur som illustrerar renormaliseringsgruppens (RG) tillvägagångssätt. När man observerar systemet på allt grövre längdskalor (indikerat med de koncentriska cirklarna och pilen framför hjärnan), minskar styrkan hos de olinjära interaktionerna (representerade av Feynman-diagrammet till vänster) endast långsamt och förblir i synnerhet skild från noll även på stora rumsliga skalor (kurva med färgade prickar). Bakgrund:samma som figur 1 men olika färgschema. Kredit:Tiberi et al.
I sin studie anpassade forskarna dessa traditionella metoder och integrerade dem med en prototypisk neuronfältmodell som först föreslogs av Wilson och Cowan. De använde dem sedan specifikt till området neurovetenskap för att undersöka kritikalitet i biologiska neurala nätverk.
"I vårt arbete studerar vi de väletablerade Wilson-Cowan-ekvationerna med stokastisk input, så modellen vi använder är inte ny," sa Tiberi, Stapmanns och deras kollegor. "Men med hjälp av RG-tekniker kommer vi fram till ett originalresultat."
För att utföra beräkningsuppgifter, kognitiva uppgifter som involverar beräkningar, måste den mänskliga hjärnan kunna memorera indata den tar emot och sedan kombinera den på komplexa sätt. Detta i sin tur gör att den kan bearbeta informationen och lösa beräkningsproblemet.
"Vi upptäckte att kritikalitet i Wilson-Cowans neurala fältmodell är av typen Gell-Mann-Low, som, bland alla typer av kritikalitet, specifikt erbjuder en optimal balans mellan att memorera indata och att kombinera dem på komplexa sätt," Tiberi, Stapmanns och deras kollegor sa.
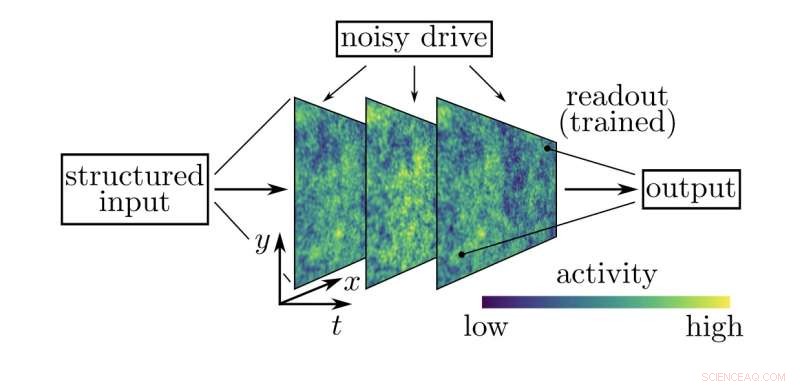
Figur som illustrerar undersökningen av modellens beräkningsförmåga. En stimulans (strukturerad ingång) läggs till systemet (med rumsliga koordinater x och y) som utvecklas genom tiden t medan nätverket också drivs av stokastisk inmatning (noisy drive). En linjär avläsning tränas för att rekonstruera eller klassificera inmatningsstimulansen från en ögonblicksbild av aktiviteten i systemet. Rekonstruktionsuppgiften testar systemets minne, medan klassificeringsuppgiften kräver olinjära interaktioner. Kredit:Tiberi et al.
Med hjälp av RG-metoder lyckades forskarna studera effekterna av olinjära interaktioner i Wilson-Cowan-modellen, som är avgörande för att förstå hur hjärnan bearbetar information. Detta är en anmärkningsvärd prestation, eftersom medelfältsmetoderna som användes av andra team tidigare inte kunde fånga dessa effekter, särskilt när interaktioner är tillräckligt starka för att forma hjärnans dynamik i en makroskopisk skala.
"Vi förväntar oss att RG-metoder kommer att vara användbara för att studera andra icke-linjära processer i neuronala nätverk," förklarade teamet. "Dessutom drar vi kopplingar till andra områden av fysiken:Begreppet Gell-Man-Låg kritikalitet härstammar från kvantfältteorin och Kardar-Parisi-Zhang-modellen, som är nära relaterad till vår modell, har ursprungligen använts för att beskriva dynamisk tillväxt av gränssnitt."
I framtiden kan teorin som introducerats av detta team av forskare användas för att undersöka olika andra hjärndynamik och neurala processer, som sträcker sig bortom kritikalitet. Dessutom skulle det i slutändan kunna bana väg mot introduktionen av andra teoretiska konstruktioner som förenar fysik och neurovetenskap.
"I hjärnan är styrkan av kopplingar mellan neuroner mycket varierande i en utsträckning att den i en första approximation kan beskrivas som slumpmässig," tillade forskarna. "Vi planerar nu att tillämpa våra metoder på neurala modeller som inkluderar denna funktion och se vilken effekt detta har, om någon, på vilken typ av kritik vi finner." + Utforska vidare
© 2022 Science X Network