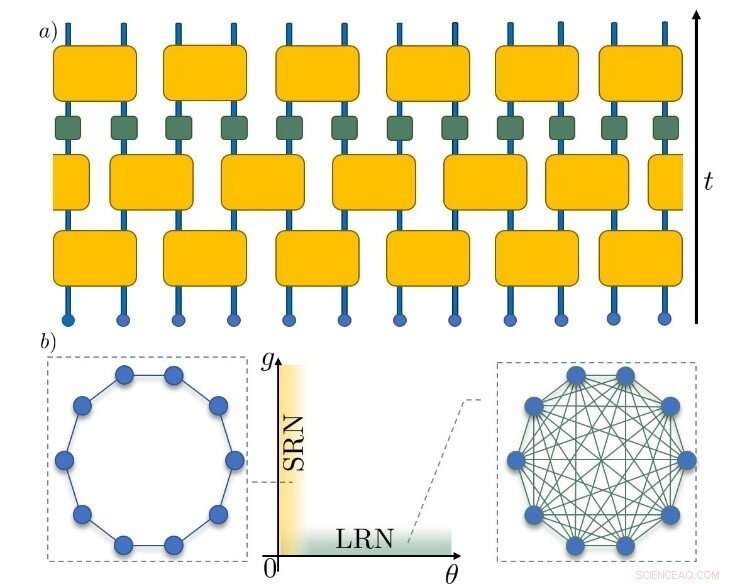
Figur 1. Schematisk representation av Unitary Circuit Map-modellen. (a) Den svarta pilen till höger visar tidens riktning när partiklarna, representerade av små blå cirklar, utvecklas. De gula rutorna representerar omvandlingarna som kopplar partiklarna. De gröna rutorna indikerar de kaosinducerande olinjära transformationerna. (b) Beroende på de valda parametrarna kan kopplingen mellan partiklarna vara av kort räckvidd (vänster) eller lång räckvidd (höger). Detta påverkar i slutändan de framväxande tidsskalorna av kaotisk dynamik. Kredit:Institutet för grundvetenskap
Ett populärt exempel på kaotiskt beteende är fjärilseffekten - en fjäril kan slå med vingarna någonstans i Atlanten och orsaka en tornado i Colorado. Denna anmärkningsvärda fabel illustrerar hur den extrema känsligheten hos dynamiken i kaotiska system kan ge dramatiskt olika resultat trots små skillnader i initiala förhållanden. De grundläggande naturlagarna som styr dynamiken i fysiska system är i sig olinjära, vilket ofta leder till kaos och efterföljande termalisering.
Men man kan fråga sig varför det inte finns någon skenande ökning av tornados i Colorado orsakad av en massiv besvikelse av fjärilar i globala angelägenheter, till exempel global uppvärmning? Detta beror på att fysisk dynamik, även om den är kaotisk, kan visa anmärkningsvärt stabila tillstånd. Ett exempel är stabiliteten i vårt solsystem – det lyder olinjära fysiklagar, vilket till synes kan framkalla kaos i systemet.
Anledningen till denna stabilitet beror på det faktum att svagt kaotiska system kan uppvisa mycket ordnad periodisk dynamik som kan pågå i miljontals år. Denna upptäckt gjordes på 1950-talet av stora matematiker Kolmogorov, Arnold och Moser. Deras upptäckt fungerar dock bara i fallet med system med ett litet antal interagerande element. Om systemet innehåller många beståndsdelar, är dess öde inte så väl förstått.
Forskare från Center for Theoretical Physics of Complex Systems (PCS) inom Institute for Basic Science (IBS), Sydkorea, har nyligen introducerat ett nytt ramverk för att karakterisera svagt kaotisk dynamik i komplexa system som innehåller ett stort antal ingående partiklar. För att uppnå detta använde de en kvantberäkningsbaserad modell – Unitary Circuits Map – för att simulera kaos.
Att undersöka kaotiska tidsskalor är en utmanande uppgift som kräver effektiva beräkningsmetoder. Unitary Circuit Map-modellen som implementerats i denna studie tillgodoser detta krav. "Modellen möjliggör effektiv och felfri spridning av tillstånd i tid", förklarar Merab Malishava, "vilket är väsentligt för att modellera extremt svag kaoticitet i stora system. Sådana modeller användes för att uppnå rekordartade olinjära evolutionstider tidigare, vilket var också gjort i vår grupp."
Som ett resultat kunde de klassificera dynamiken i systemet genom att identifiera tids- och längdskalor som uppstår när termaliseringen dras långsammare. Forskarna fann att om de ingående delarna är anslutna på ett långt räckviddsnät (LRN) sätt (till exempel på ett allt-till-alla-sätt), så kännetecknas termaliseringsdynamiken av en unik tidsskala, kallad Lyapunov-tiden. Men om kopplingen är av kortdistansnät (SRN) karaktär (till exempel närmaste granne) uppstår en ytterligare längdskala relaterad till frysning av större delar av systemet under långa tider med sällsynta kaotiska stänk.
Typiskt görs studierna på sådan känslig dynamik med hjälp av tekniker för att analysera beteendet hos observerbara objekt. Dessa tekniker går tillbaka till 1950-talet när de första experimenten med kaotiskhet och termalisering utfördes. Författarna identifierade en ny analysmetod – genom att undersöka Lyapunovs spektrumskalning.
Merab Malishava säger:"Tidigare metoder kan resultera i tvetydiga resultat. Du väljer en observerbar och till synes märker termalisering och tror att dynamiken är kaotisk. Men om en annan observerbar studeras, från ett annat perspektiv, drar du slutsatsen att systemet är fruset och ingenting förändringar, vilket betyder ingen termalisering. Detta är tvetydigheten som vi övervann. Lyapunov-spektrumet är en uppsättning tidsskalor som karaktäriserar dynamiken fullständigt och fullständigt. Och vad mer är, det är samma ur alla synvinklar! Unikt och entydigt."
Resultaten är inte bara intressanta ur en grundläggande synvinkel. De har också potential att belysa kvantdatorernas förverkliganden. Kvantberäkning kräver koherent dynamik, vilket innebär ingen termalisering. I det aktuella arbetet studerades en dramatisk avmattning av termisk dynamik med framväxande kvasikonserverade storheter. Att kvantifiera detta fall skulle möjligen kunna förklara sådana fenomen som många kroppslokalisering, vilket är en av grundidéerna för att undvika termalisering i kvantdatorer.
En annan stor prestation av studien relaterar till tillämpbarheten av resultaten på en stor majoritet av fysiska modeller, allt från enkla oscillatornätverk till komplex spinnnätverksdynamik. Dr. Sergej Flach, ledaren för forskargruppen och chefen för PCS förklarar:"Vi har arbetat i fem år med att utveckla ett ramverk för att klassificera svagt kaotisk dynamik i makroskopiska system, vilket resulterade i en serie arbeten som avsevärt utvecklade området. . Vi lägger åt sidan snävt fokuserade fall-till-fall-studier till förmån för att främja ett konceptuellt tillvägagångssätt som är tillförlitligt och relaterbart i ett stort antal fysiska realiseringar. Detta specifika arbete är en mycket viktig byggsten i det ovannämnda ramverket. Vi fann att en Det traditionella sättet att se på saker är ibland inte det mest informativa och erbjuder ett nytt alternativt tillvägagångssätt. Vårt arbete stannar inte här, eftersom vi ser fram emot att utveckla vetenskapen med fler banbrytande idéer."
Denna forskning publicerades nyligen i Physical Review Letters. + Utforska vidare