Många av dagens kvantenheter förlitar sig på samlingar av qubits, även kallade spins. Dessa kvantbitar har bara två energinivåer, "0" och "1". Men snurr i riktiga enheter interagerar också med ljus och vibrationer som kallas bosoner, vilket i hög grad komplicerar beräkningar.
I en ny publikation i Physical Review Letters , demonstrerar forskare i Amsterdam ett sätt att beskriva spin-boson-system och använda detta för att effektivt konfigurera kvantenheter i önskat tillstånd.
Kvantenheter använder kvantpartiklarnas egendomliga beteende för att utföra uppgifter som går utöver vad "klassiska" maskiner kan göra, inklusive kvantberäkning, simulering, avkänning, kommunikation och metrologi. Dessa enheter kan ta många former, till exempel en samling supraledande kretsar eller ett gitter av atomer eller joner som hålls på plats av lasrar eller elektriska fält.
Oavsett deras fysiska realisering beskrivs kvantenheter vanligtvis i förenklade termer som en samling av interagerande kvantbitar eller snurr på två nivåer. Dessa spinn interagerar dock också med andra saker i sin omgivning, som ljus i supraledande kretsar eller svängningar i atomernas eller jonernas gitter. Partiklar av ljus (fotoner) och vibrationslägen i ett gitter (fononer) är exempel på bosoner.
Till skillnad från snurr, som bara har två möjliga energinivåer ("0" eller "1"), är antalet nivåer för varje boson oändligt. Följaktligen finns det väldigt få beräkningsverktyg för att beskriva snurr kopplade till bosoner.
I sitt nya arbete arbetar fysikerna Liam Bond, Arghavan Safavi-Naini och Jiří Minář vid University of Amsterdam, QuSoft och Centrum Wiskunde &Informatica kring denna begränsning genom att beskriva system som består av spinn och bosoner som använder så kallade icke-Gaussiska tillstånd. Varje icke-Gaussisk stat är en kombination (en överlagring) av mycket enklare Gaussiska tillstånd.
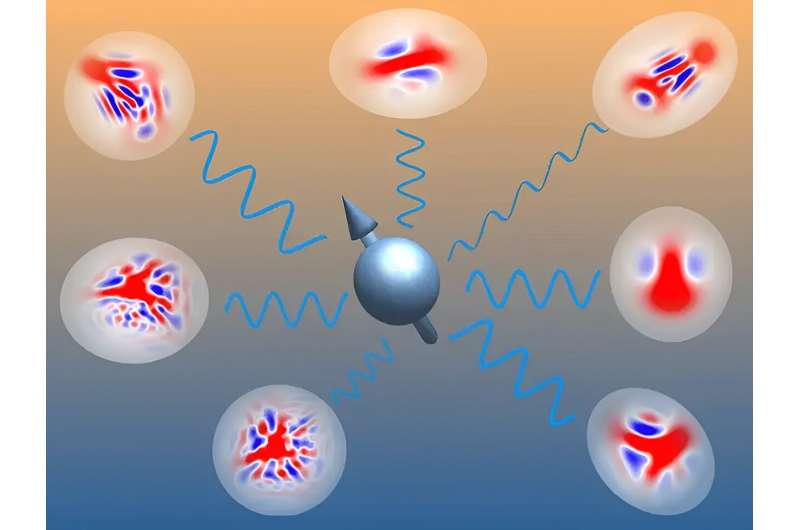
Varje blårött mönster i bilden ovan representerar ett möjligt kvanttillstånd för spin-bosonsystemet. "En Gaussisk stat skulle se ut som en vanlig röd cirkel, utan några intressanta blå-röda mönster", förklarar Ph.D. kandidat Liam Bond. Ett exempel på ett Gaussiskt tillstånd är laserljus, där alla ljusvågor är perfekt synkroniserade.
"Om vi tar många av dessa Gaussiska tillstånd och börjar överlappa dem (så att de är i en superposition), kommer dessa vackert intrikata mönster fram. Vi var särskilt glada eftersom dessa icke-Gaussiska stater tillåter oss att behålla mycket av den kraftfulla matematiska maskineri som finns för Gaussiska tillstånd, samtidigt som det gör det möjligt för oss att beskriva en mycket mer mångsidig uppsättning kvanttillstånd, säger Bond.
"Det finns så många möjliga mönster att klassiska datorer ofta kämpar för att beräkna och bearbeta dem. Istället använder vi i denna publikation en metod som identifierar de viktigaste av dessa mönster och ignorerar de andra. Detta låter oss studera dessa kvantsystem och designa nya sätt att förbereda intressanta kvanttillstånd."
Den nya metoden kan utnyttjas för att effektivt förbereda kvanttillstånd på ett sätt som överträffar andra traditionellt använda protokoll. "Snabb förberedelse av kvanttillstånd kan vara användbar för ett brett spektrum av applikationer, såsom kvantsimulering eller till och med kvantfelskorrigering", konstaterar Bond.
Forskarna visar också att de kan använda icke-Gaussiska tillstånd för att förbereda "kritiska" kvanttillstånd som motsvarar ett system som genomgår en fasövergång. Förutom grundläggande intresse kan sådana tillstånd avsevärt förbättra kvantsensorernas känslighet.
Även om dessa resultat är mycket uppmuntrande, är de bara ett första steg mot mer ambitiösa mål. Hittills har metoden demonstrerats för ett enda snurr. En naturlig, men utmanande förlängning är att inkludera många snurr och många bosoniska lägen på samma gång. En parallell riktning är att ta hänsyn till effekterna av miljön som stör spin-bosonsystemen. Båda dessa tillvägagångssätt är under aktiv utveckling.