Att utforska vågutbredning och lokalisering i olika medier har varit ett centralt fokus inom optik och akustik. Specifikt, inom fotonik och fononi, har forskare varit dedikerade till att förstå och kontrollera beteendet hos ljus och ljudvågor i periodiska medier.
Med sina unika bandgap-egenskaper erbjuder fotoniska kristaller en utmärkt plattform för att studera vågutbredning och lokalisering. Dessa bandgap, orsakade av kristallens periodiska struktur, kan styra vågutbredning och till och med helt hämma vågor i vissa frekvensområden.
Traditionellt trodde man att gränslägen i fotoniska kristaller påverkas starkt av storleken på kristallen (antal gitterplatser). Det antogs allmänt att dessa lägen är lättare att begränsa i stora system (med många gitterplatser) eftersom sannolikheten för tunnling minskar avsevärt med ökande systemstorlek. Detta fenomen är avgörande för att designa och implementera högpresterande fotoniska enheter, särskilt när det gäller att sträva efter hög integration och miniatyrisering av enheter.
Dessutom, inom fotonisk kristallforskning, har bundna tillstånd i kontinuum (BIC) väckt uppmärksamhet eftersom de avslöjar att vissa unika lägen kan begränsas inom specifika regioner även i det kontinuerliga spektrumet. Detta fenomen ger ett nytt perspektiv för att förstå och kontrollera lokaliseringen av ljusvågor. Det visar på stor potential i praktiska tillämpningar, som att förbättra prestanda och effektivitet hos optiska enheter.
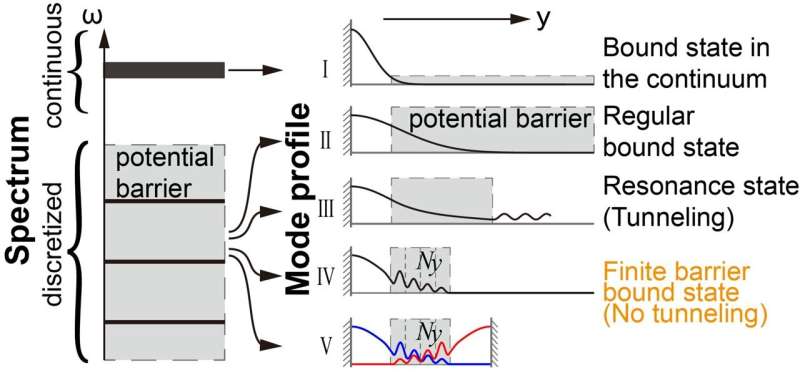
Ny forskning publicerad i Light:Science &Applications föreslår och bekräftar förekomsten av ändliga barriärbundna tillstånd. Spektrumet för ett system består typiskt av kontinuerliga och diskreta spektra (vänster panel i fig. 1). Konventionell visdom hävdar att egenvärdesspektrumet för bundna tillstånd är diskret, medan obundna tillstånd bildar ett kontinuerligt spektrum.
Till exempel, i elektroniska system, om partikelns energi är lägre än den potentiella energin i oändligheten, är tillståndet bundet med ett diskret spektrum; medan partiklar med högre energi än den potentiella energin sprider sig och bildar ett kontinuerligt spektrum.
För ljus- och ljudvågor bildas diskreta tillstånd på grund av gränsförhållanden som åläggs av en barriär, såsom ett "bandgap". Dessa diskreta tillstånd kan lokaliseras helt under idealiska förhållanden (oändlig barriärbredd, fig. 1-II). Men när barriärens bredd är ändlig, finns det en sannolikhet för tillståndet att tunnla genom barriären och bli ett resonant tillstånd (Fig. 1-III).
Noterbart är att bundna tillstånd i kontinuum (BIC) är spatialt bundna inom det kontinuerliga spektrumets energi/frekvensområde (fig. 1-I). Denna studie introducerar ett kontraintuitivt koncept parallellt med BIC:er:vissa tillstånd kan bindas helt och hållet i mycket tunna bandgapmaterial, vilket gör dem oförmögna att tunnla genom bandgapmaterialet (fig. 1-IV och 1-V).
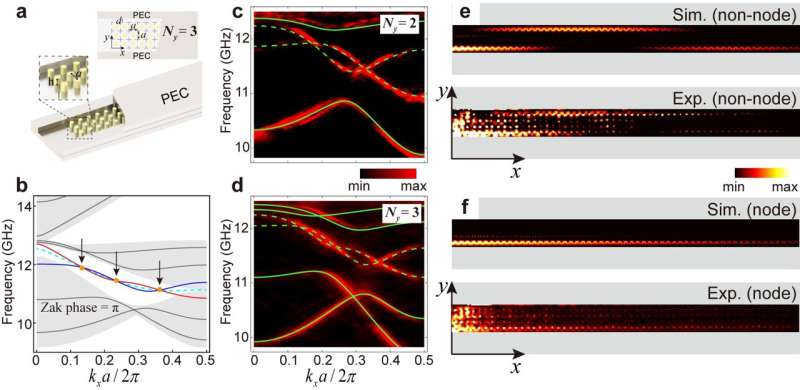
Studien demonstrerar först en speciell spegelsymmetrisk fotonisk kristallremsstruktur där övergången av gränslägen kan fint kontrolleras. När bredden på den fotoniska kristallen (antalet gitterplatser längs y-riktningen, Ny ) är liten, gränslägena på båda sidor samverkar och delas upp i udda och jämna lägen (Fig. 2 a–d).
Vid specifika vågvektorer (noder) är kopplingsstyrkan för gränslägena noll. Även om bredden (Ny ) av den fotoniska kristallen är mycket liten, kan gränsläget inte hoppa från ena sidan av den fotoniska kristallen till den andra (fig. 2 e–f). I allmänhet antas det att många gitterställen krävs för att undertrycka kopplingen av gränsmoder. Ändå utmanar denna studie denna syn och öppnar en ny metod för att manipulera fotonbeteende i mikroskopisk skala.
Efter den tidigare konfigurationen tar forskare bort en PEC-gräns för den fotoniska kristallen, vilket avslöjar en ny konfiguration. De upptäckte att de återstående gränslägena vid specifika nodalvågsvektorer är helt fångade, vilket bildar Finite Barrier Enabled Bound States in the Continuum (FBICs).
Dessa FBICs uppvisar icke-strålande egenskaper på grund av frikopplingen av de två gränslägena. Vid noderna, där kopplingsstyrkan för gränslägen är noll, existerar ett tillstånd med en strålningskoefficient på noll när en sida av PEC tas bort, och dess frekvens matchar nodfrekvensen som finns i det dubbla PEC-scenariot, vilket identifierar den som en FBIC.
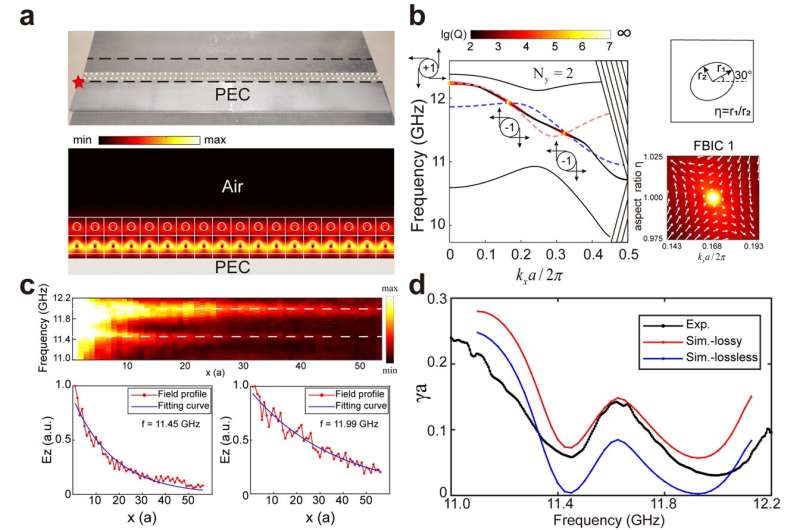
Dessutom, genom att ändra det cirkulära dielektrikumet till elliptiskt för att bryta den ursprungliga spegelsymmetrin och introducera en ny geometrisk parameter η, definierade studien ett lindningsnummer i kx-η-parameterutrymmet, avslöjar de topologiska egenskaperna hos FBIC:er och bekräftar dessa lägen som BIC:er ( Fig. 3 a–b).
Med tanke på den oundvikliga dielektriska förlusten vid mikrovågsfrekvenser, validerade studien experimentellt FBIC:er genom att mäta dämpningen av gränslägen (Fig. 3 c–d), vilket visar fullständig lokalisering av gränslägen inom mycket få gitterplatser (Ny =2, 3, etc.), som erbjuder en ny metod för att uppnå BIC.
Denna banbrytande studie utforskar nya fysiska fenomen i fotoniska kristaller och uppnår fin kontroll av gränslägen. Detta arbete ger inte bara en ny förståelse av tunnling och begränsning av gränslägen i fotoniska kristaller teoretiskt utan bekräftar också den fullständiga lokaliseringen av gränslägen vid specifika vågvektorer genom mikrovågsexperiment, vilket ger ett nytt perspektiv till fotonikområdet.
Forskningen avslöjar nya metoder för att manipulera fotonbeteende, vilket är viktigt för att utveckla högintegrerade fotoniska enheter. Det erbjuder också nya strategier för att använda fotoniska kristaller för att förbättra ljus-materia-interaktioner, vilket kan leda till genombrott inom olinjär optik och interaktioner mellan ljus och tvådimensionella material. Dessa fynd kan inspirera framtida forskning, som att tillämpa dessa principer på andra vågsystem som fononiska kristaller.
Mer information: Tao Liu et al, Finite barriärbundet tillstånd, Light:Science &Applications (2024). DOI:10.1038/s41377-024-01417-1
Journalinformation: Ljus:Vetenskap och tillämpningar
Tillhandahålls av TranSpread