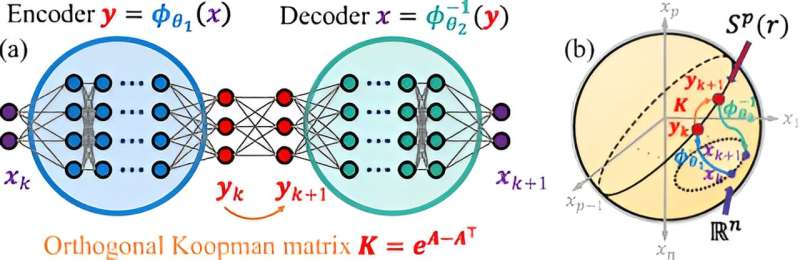
I en ny utveckling vid Fudan University har ett team av tillämpade matematiker och AI-forskare avslöjat ett banbrytande ramverk för maskininlärning designat för att revolutionera förståelsen och förutsägelsen av Hamiltonska system. Artikeln är publicerad i tidskriften Physical Review Research .

Detta innovativa ramverk, kallat Hamiltonian Neural Koopman Operator (HNKO), integrerar principer för matematisk fysik för att rekonstruera och förutsäga Hamiltonska system med extremt höga dimensioner med hjälp av bullriga eller delvis observerade data.

HNKO-ramverket, utrustat med en enhetlig Koopman-struktur, har den anmärkningsvärda förmågan att upptäcka nya bevarandelagar enbart från observationsdata. Denna förmåga tar itu med en betydande utmaning när det gäller att exakt förutsäga dynamik i närvaro av brusstörningar, vilket markerar ett stort genombrott inom Hamiltons mekanik.

Forskare vid Fudan University visade upp kraften i HNKO och dess förlängningar genom att tillämpa den på en rad fysiska modeller, inklusive himmelska n-kroppssystem med hundratals och tusentals frihetsgrader.

Deras numeriska experiment visade ramverkets effektivitet i att skala till komplexa fysiska system, vilket bekräftade dess potential att revolutionera förståelsen av komplexa dynamiska system.

Denna prestation understryker vikten av att införliva förkunskaper och matematisk teori i ramverk för maskininlärning, vilket avsevärt förbättrar deras förmåga att lösa intrikata fysiska problem. Fudan Universitys banbrytande arbete innebär ett avgörande steg framåt i att utnyttja artificiell intelligens för att främja vår förståelse av grundläggande fysik och matematik.

Mer information: Jingdong Zhang et al, Lärande Hamiltonian neural Koopman-operatör och samtidigt upprätthålla och upptäcka bevarandelagar, Physical Review Research (2024). DOI:10.1103/PhysRevResearch.6.L012031

Journalinformation: Fysisk granskning

Tillhandahålls av Fudan University