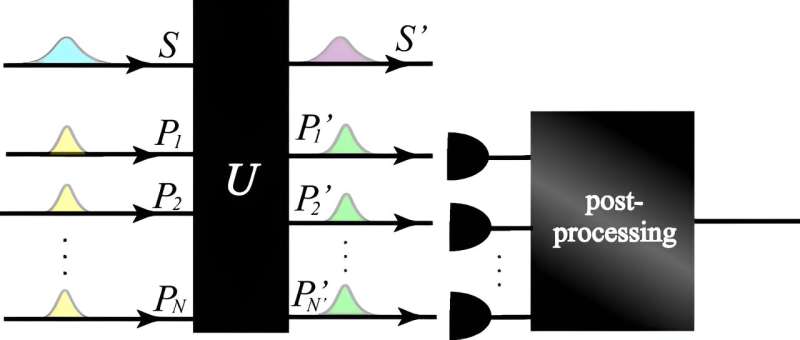
En studie publicerad i tidskriften Physical Review Letters av forskare i Japan löser ett långvarigt problem inom kvantfysik genom att omdefiniera osäkerhetsprincipen.

Werner Heisenbergs osäkerhetsprincip är ett centralt och överraskande inslag i kvantmekaniken, och det kan han tacka sin hösnuva för. Miserabel i Berlin sommaren 1925 semestrade den unge tyske fysikern på den avlägsna, klippiga ön Helgoland, i Nordsjön utanför den nordtyska kusten. Hans allergier förbättrades, och han kunde fortsätta sitt arbete med att försöka förstå krångligheterna i Bohrs modell av atomen, utveckla tabeller över inre atomegenskaper, såsom energi, position och momentum.

När han återvände till Göttingen, insåg hans rådgivare, Max Born, att dessa tabeller var och en kunde formas till en matris - i huvudsak en tvådimensionell värdetabell. Tillsammans med den 22-årige Pasqual Jordan förfinade de sitt arbete till matrismekanik – den första framgångsrika teorin om kvantmekanik – de fysiska lagarna som beskriver små föremål som atomer och elektroner.

Medan matrismekaniken inom några år skulle ersättas av Schrödingers vågfunktion och hans ekvation, tillät den Heisenberg insikten att formulera osäkerhetsprincipen:det finns en gräns för hur exakt platsen och momentumet för ett kvantsystem, vanligtvis en partikel, kan vara uppmätt.

Gränsen för produkten av mätosäkerheterna för de två storheterna är h/4π, där h är Planck-konstanten, extremt liten men inte desto mindre inte noll. Kort sagt, man kan inte mäta både positionen och rörelsemängden för ett kvantobjekt med godtycklig precision – att mäta det ena med högre precision innebär att det andra bara kan mätas med lägre precision.

I en fysisk syn, anta att vi vill mäta positionen och rörelsemängden för en elektron. Man måste lysa av något slag på ett system för att mäta dess egenskaper. Ljus kvantiseras som fotoner, som har en energi som inte är noll. Att lysa en foton på elektronen stör nödvändigtvis elektronen från dess ursprungliga tillstånd. Inom kvantmekaniken sätter bara mätningen en gräns för mätningens precision.

Liknande osäkerheter gäller för mätningar av tid och energi, och vinkelposition och rörelsemängd, och i allmänhet alla två variabler som inte "pendlar" när de representeras som operatorer i rigorös kvantmekanik.

Några decennier senare förfinades osäkerhetsprincipen av fysikerna Eugene Wigner, sedan Huzihiro Araki och Mutsuo M. Yanase till Wigner-Araki-Yanase (WAY) satsen, som säger att för två observerbara storheter q och p, där p bevaras ( såsom rörelsemängd i ett system), så även om p inte mäts alls, kan q inte mätas med godtycklig precision.

"Som en konsekvens av WAY-satsen kan vi se att det (i en viss mening) är omöjligt att mäta partikelns position q; allt vi kan mäta är dess position i förhållande till apparaten, q—Q," matematiker John Baez från University of California, Riverside har skrivit, där Q är positionen för mätapparaten.

Men WAY-satsen gällde bara kvantiteter som ett partikelspin, som bara kan ta diskreta och avgränsade kvantiteter.

Nu har Yui Kuramochi från Kyushu University och Hiroyasu Tajima från University of Electro-Communications i Japan löst ett långvarigt problem genom att visa att WAY-satsen även gäller observerbara storheter som är kontinuerliga (inte diskreta) eller obegränsade, såsom position.

"Enligt osäkerhetsprincipen kan position och momentum inte mätas exakt samtidigt", säger Kuramochi. "Vårt resultat ger en ytterligare begränsning:inte ens själva positionen kan mätas exakt, så länge vi använder naturliga mätningar som uppfyller momentumbevarandet." Deras bevis undersöker en "obegränsad operator", fysiska storheter som kan ta oändligt stora värden.

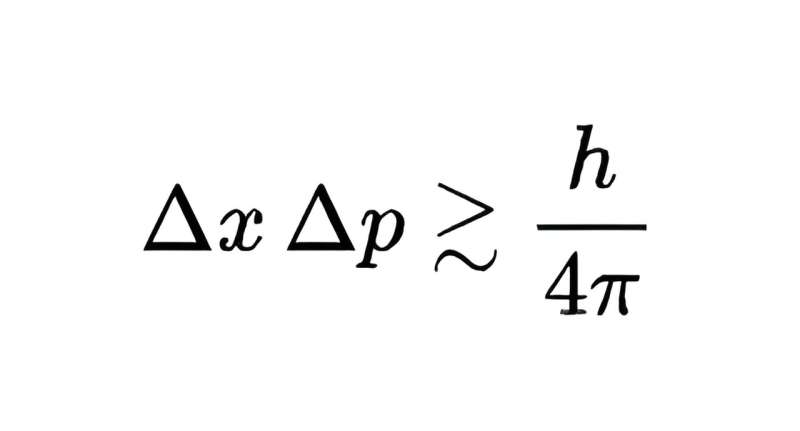
Strängt taget kräver resultatet ett särskilt tillstånd som ligger till grund för WAY-satsen, kallat Yanase-villkoret. Även om det är mycket tekniskt, fastställer det i huvudsak kompatibiliteten för apparatens obegränsade variabel med den bevarade kvantiteten. Yanase-tillståndet, även om det är matematiskt, verkar önskat av tillämpningar på verkliga fysiska system.

"WAY-satsen förutspår att enligt en bevarandelag kan en fysisk kvantitet som inte pendlar med den bevarade laddningen inte mätas utan fel", fortsätter Kuramochi. "Detta motsvarar ett svar på ett 60-årigt öppet problem. Det nya resultatet löser ett årtionden gammalt problem om hur man närmar sig sådana kontinuerliga och obegränsade observerbara objekt, särskilt inom områden som kvantoptik, där den nya satsförlängningen sannolikt kommer att hitta tillämpningar ."

Den ursprungliga WAY-satsen förbjuder att mätfelet är noll, men det är en kvalitativ sats och anger inte mätgränsen eller ens om det finns en nedre gräns som är större än noll. Detsamma gäller för denna WAY-satsförlängning av Kuramochi och Tajima.

I sin artikel skriver författarna att det fortfarande är en öppen fråga om den ursprungliga WAY-satsen för upprepade mätningar kan generaliseras som de har, till obegränsade bevarade observerbara objekt.

Genom att föreslå nya riktningar för undersökningar av förlängningar av WAY-satsen, skulle teamet vilja generalisera sina resultat till energibegränsade tillstånd, eftersom deras nuvarande resultat är begränsade till tillståndsoberoende fall och till approximativa fall. En potentiell tillämpning är att sätta gränser för hur kvantnätverksöverföringsprotokoll kan prestera bättre än klassiska gränser.

Mer information: Yui Kuramochi et al, Wigner-Araki-Yanase-satsen för kontinuerliga och obegränsade bevarade observerbara objekt, Physical Review Letters (2023). DOI:10.1103/PhysRevLett.131.210201

Journalinformation: Fysiska granskningsbrev

© 2023 Science X Network