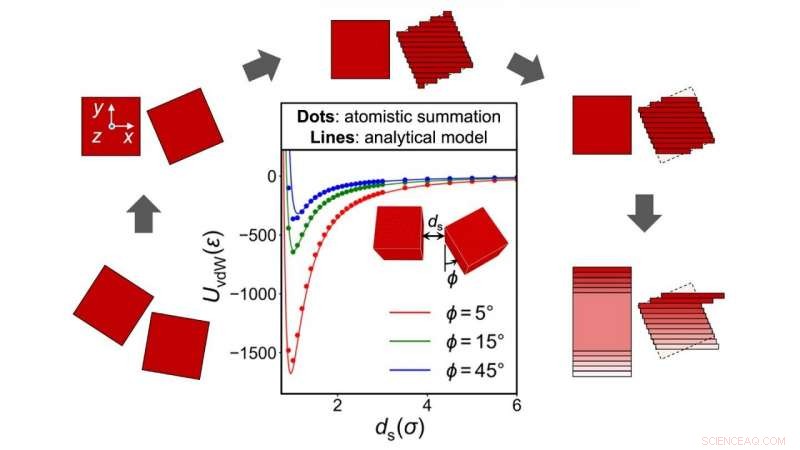
Översikt över tillvägagångssättet som används för att härleda analytiska uttryck för interpartikeln van der Waals interaktionspotential för facetterade nanopartiklar. Modellen går igenom en rad förenklingar. Ett block är normaliserat i ett standardläge. Det andra blocket antas då vara en gruppering av stavar. Eventuella stavar utanför det första blockets gränser antas vara försumbara. Det första blocket skiftas för att centreras på varje stång i det andra blocket medan dess krafter beräknas och summeras. Kredit:Gaurav Arya, Duke University
Materialforskare vid Duke University har tagit fram en förenklad metod för att beräkna de attraktionskrafter som gör att nanopartiklar självmonterar sig till större strukturer.
Med denna nya modell, åtföljs av ett grafiskt användargränssnitt som visar dess kraft, forskare kommer att kunna göra tidigare omöjliga förutsägelser om hur nanopartiklar med en mängd olika former kommer att interagera med varandra. Den nya metoden erbjuder möjligheter att rationellt designa sådana partiklar för ett brett spektrum av tillämpningar från att utnyttja solenergi till att driva katalytiska reaktioner.
Resultaten visas online den 12 november i tidskriften Nanoskala horisonter.
"Faceterade nanopartiklar kan leda till nya monteringsbeteenden, som inte har utforskats tidigare, sa Brian Hyun-jong Lee, en doktorand i maskinteknik och materialvetenskap vid Duke och första författare till tidningen. "Kuber, prismor, stavar och så vidare uppvisar alla distinkta avstånds- och orienteringsberoende interpartikelinteraktioner som kan användas för att skapa unika partikelaggregat som man inte kan erhålla genom självmontering av sfäriska partiklar."
"Varje gång jag går igenom den senaste uppsättningen publicerade artiklar inom nanoteknik, Jag ser några nya tillämpningar av dessa typer av nanopartiklar, " lade Gaurav Arya till, docent i maskinteknik och materialvetenskap vid Duke. "Men att noggrant beräkna krafterna som drar ihop dessa partiklar på mycket nära håll är extremt beräkningsmässigt dyrt. Vi har nu visat ett tillvägagångssätt som snabbar upp dessa beräkningar miljontals gånger samtidigt som det bara förlorar en liten mängd noggrannhet."
De krafter som verkar mellan nanopartiklar kallas van der Waals-krafter. Dessa krafter uppstår på grund av små, tillfälliga förändringar i tätheten hos elektroner som kretsar kring atomer enligt kvantfysikens komplexa lagar. Även om dessa krafter är svagare än andra intermolekylära interaktioner som coulombiska krafter och vätebindningar, de är allestädes närvarande och verkar mellan varje atom, dominerar ofta nettointeraktionen mellan partiklar.
För att korrekt redogöra för sådana krafter mellan partiklar, man måste beräkna van der Waals-kraften som varje atom i partikeln utövar på varje atom i en närliggande partikel. Även om båda partiklarna i fråga var små kuber av storlekar mindre än 10 nanometer, antalet beräkningar som summerar alla sådana interatomära interaktioner skulle vara i tiotals miljoner.
Det är lätt att förstå varför det snabbt blir omöjligt att försöka göra detta om och om igen för tusentals partiklar som befinner sig på olika positioner och i olika orienteringar i en multipartikelsimulering.
"Mycket arbete har gjorts för att formulera en summering som närmar sig en analytisk lösning, ", sa Arya. "Vissa metoder behandlar partiklar som består av oändligt små kuber som sitter ihop. Andra försöker fylla utrymmet med oändligt tunna cirkulära ringar. Även om dessa volymdiskretiseringsstrategier har gjort det möjligt för forskare att få analytiska lösningar för interaktioner mellan enkla partikelgeometrier som parallella plana ytor eller sfäriska partiklar, sådana strategier kan inte användas för att förenkla interaktionerna mellan fasetterade partiklar på grund av deras mer komplexa geometrier."
För att komma runt det här problemet, Lee och Arya tog ett annat tillvägagångssätt genom att göra flera förenklingar. Det första steget innebär att representera partikeln som inte uppbyggd av kubiska element, men av stavformade element av olika längder staplade ihop. Modellen antar då att stavar vars projektioner faller utanför den projicerade gränsen för den andra partikeln bidrar försumbart till den totala interaktionsenergin.
Energierna som de återstående stavarna bidrar med antas vidare vara lika med energierna för stavar med enhetlig längd som ligger på samma normala avstånd som de faktiska stavarna, men med noll sidoförskjutning. Det sista tricket är att approximera avståndsberoendet för stav-partikelenergin med hjälp av kraftlagsfunktioner som har lösningar i sluten form när avstånden varierar linjärt med den laterala positionen för de faktiska stavarna, som är fallet med de plana samverkande ytorna av facetterade partiklar.
Efter att alla dessa förenklingar har gjorts, analytiska lösningar för interpartikelenergierna kan erhållas, så att en dator kan blåsa igenom dem. Och även om det kan låta som att de skulle introducera en stor mängd fel, forskarna fann att resultaten endast var 8 % rabatt i genomsnitt från det faktiska svaret för alla partikelkonfigurationer, och bara 25 % olika när de är som värst.
Medan forskarna främst arbetade med kuber, de visade också att tillvägagångssättet fungerar med triangulära prismor, fyrkantiga stavar och fyrkantiga pyramider. Beroende på nanopartiklarnas form och material, Modelleringsmetoden kan påverka ett brett spektrum av områden. Till exempel, silver eller guld nanokuber med kanter nära varandra kan utnyttja och fokusera ljus till små "hotspots, " skapa en möjlighet för bättre sensorer eller katalysera kemiska reaktioner.
"Detta är första gången som någon har föreslagit en analytisk modell för van der Waals interaktioner mellan facetterade partiklar, ", sa Arya. "Även om vi ännu inte har tillämpat det för att beräkna interpartikelkrafter eller energier inom molekylär dynamik eller Monte Carlo-simuleringar av partikelsammansättning, vi förväntar oss att modellen ska påskynda sådana simuleringar med så mycket som tio storleksordningar."