Den här artikeln visar hur man skisserar graferna för kvadratrotsfunktionen genom att använda endast tre olika värden för "x" och sedan hitta punkterna genom vilka grafen för ekvationerna /funktionerna ritas, det visar också hur graferna Vertikalt translaterar (flyttas uppåt eller nedåt), översätts horisontellt (flyttas åt vänster eller till höger) och hur grafen samtidigt gör båda översättningarna.
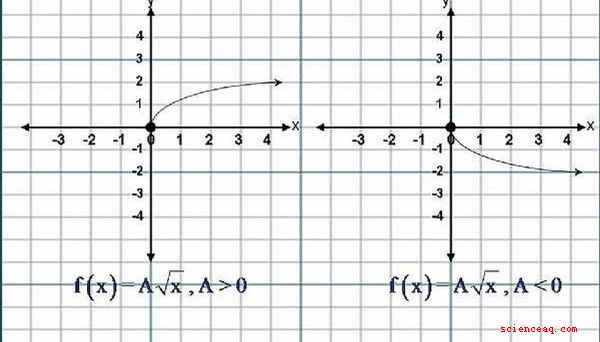
Ekvationen för en kvadratrotsfunktion har formuläret, .. . y = f (x) = A√x, där (A) får inte vara lika med noll (0). Om (A) är större än Noll (0), är (A) ett positivt tal, sedan Form av graden av kvadratrotsfunktionen liknar den övre halvan av bokstaven, 'C'. Om (A) är Mindre än noll (0), dvs (A) är ett negativt tal, liknar formens form den som i den nedre halvan av bokstaven "C". Vänligen klicka på bilden för en bättre vy.
För att skissera ekvationsgrafen, ... y = f (x) = A√x, väljer vi tre värden för 'x', x = ( -1), x = (0) och x = (1). Vi ersätter varje värde av "x" till ekvationen, ... y = f (x) = A√x och får motsvarande värde för varje "y".
Med tanke på y = f (x) = A√x, där (A) är ett reellt tal och (A) inte lika med noll (0) och ersätter x = (-1) i ekvationen får vi y = f (-1) = A√ -1) = i (vilket är ett imaginärt tal). Så den första punkten har inga riktiga koordinater, därför kan ingen graf dras genom denna punkt. Nu ersätter x = (0) får vi y = f (0) = A√ (0) = A (0) = 0. Så den andra punkten har koordinater (0,0). Och ersätter x = (1) vi får y = f (1) = A√ (1) = A (1) = A. Så den tredje punkten har koordinater (1, A). Eftersom den första punkten hade koordinater som inte var riktiga, letar vi nu efter en fjärde punkt och väljer x = (2). Nu ersätt x = (2) till y = f (2) = A√ (2) = A (1,41) = 1,41A. Så den fjärde punkten har koordinater (2,1,41A). Vi skisserar nu kurvan genom dessa tre punkter. Vänligen klicka på bilden för en bättre vy.
Med tanke på ekvationen y = f (x) = A√x + B, där B är ett verkligt tal, skulle grafen för denna ekvation översätt vertikalt (B) enheter. Om (B) är ett positivt tal kommer grafen att flytta upp (B) -enheter, och om (B) är ett negativt tal kommer grafen att flytta ner (B) -enheter. För att skissa graferna för denna ekvation följer vi anvisningarna och använder samma värden för "x" i steg # 3. Vänligen klicka på bilden för att få en bättre bild.
Med tanke på ekvationen y = f (x) = A√ (x - B) där A och B är några reella tal och (A) inte lika med Noll (0) och x ≥ B. Grafen för denna ekvation skulle översätta horisontellt (B) -enheter. Om (B) är ett positivt tal flyttas grafen till höger (B) -enheterna och om (B) är ett negativt tal flyttas grafen till vänster (B) -enheterna. För att skissa graferna för denna ekvation sätter vi först uttrycket 'x - b' som ligger under det radikala tecknet Större än eller lika till noll och lösa för 'x'. Det vill säga, ... x - B ≥ 0, sedan x ≥ B.
Vi använder nu följande tre värden för x, x = (B), x = (B + 1) och x = (B + 2). Vi ersätter varje värde av "x" till ekvationen, ... y = f (x) = A√ (x - B) och får motsvarande värde för varje "y".
Givet y = f (x) = A√ (x - B), där A och B är reella tal och (A) inte lika med noll (o) där x ≥ B. Att ersätta x = (B) i ekvationen vi får y = f (B) = A√ (BB) = A√ (0) = A (0) = 0. Så den första punkten har koordinater (B, 0). Nu ersätter x = (B + 1) får vi y = f (B + 1) = A√ (B + 1 - B) = A√1 = A (1) = A. Så den andra punkten har koordinater B + 1, A) och ersätter x = (B + 2) får vi y = f (B + 2) = A√ (B + 2-B) = A√ (2) = A (1,41) = 1,41A . Så den tredje punkten har koordinater (B + 2,1,41A). Vi skisserar nu kurvan genom dessa tre punkter. Vänligen klicka på bilden för en bättre vy.
Med tanke på y = f (x) = A√ (x - B) + C, där A, B, C är reella tal och (A) inte lika med Noll (0) och x ≥ B. Om C är ett positivt tal kommer grafen i STEG # 7 att översätta vertikalt (C) -enheter. Om (C) är ett positivt tal kommer grafen att flytta upp (C) -enheter, och om (C) är ett negativt tal, kommer graven att flytta ner (C) -enheter. För att skissa graferna för denna ekvation följer vi anvisningarna och använder samma värden för "x" i steg # 7. Vänligen klicka på bilden för att få en bättre bild.