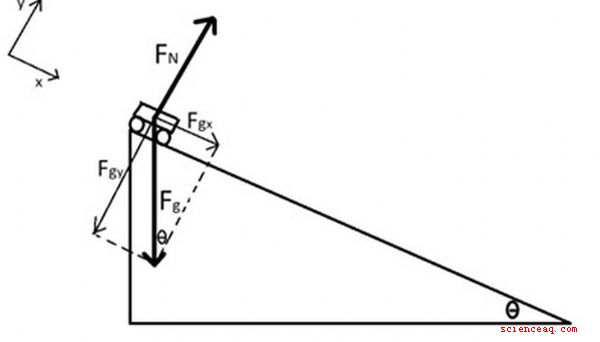
nettokraften
är vektorsumman för alla krafter som verkar på en kropp. (Kom ihåg att en kraft är en push eller en pull.) SI-enheten för kraft är Newton (N), där 1 N \u003d 1 kgm /s ^{2.
\\ bold {F_ {net}} \u003d \\ bold {F_1 + F_2 + F_3 + ...}}

Newtons första lag säger att ett objekt som genomgår enhetlig rörelse - vilket betyder att det är i vila eller rör sig med konstant hastighet - kommer att fortsätta att göra det såvida det inte agerar av ett icke-nät tvinga. Newtons andra lag säger uttryckligen hur rörelsen kommer att förändras till följd av denna nettokraft:
\\ bold {F_ {net}} \u003d m \\ bold {a}

Accelerationen - förändring i hastighet över tid - är direkt proportionell mot nettokraften. Observera också att både acceleration och nettokraft är vektorkvantiteter som pekar i samma riktning.

TL; DR (för lång; läste inte).

En nettokraft på noll INTE nödvändigtvis menar att objektet är stoppat! En nettokraft på noll betyder inte heller att det inte finns några krafter som verkar på ett objekt eftersom det är möjligt för flera krafter att agera på ett sådant sätt att de avbryter varandra.
Free-Body Diagrams <

Det första steget i att hitta nettokraft på ett objekt är att rita ett frikroppsdiagram (FBD) som visar alla krafter som verkar på det objektet. Detta görs genom att representera varje kraftvektor som en pil som kommer från objektets centrum och pekar i den riktning som kraften verkar.

Antag till exempel att en bok sitter på ett bord. De krafter som verkar på den skulle vara tyngdkraften på boken, agera neråt och normalkraften på bordet på boken, agera uppåt. Frikroppsdiagrammet för det här scenariot skulle bestå av två pilar med samma längd som härstammar från mitten av boken, den ena pekar uppåt och den andra pekar neråt. samma bok pressades till höger med en kraft på 5 N medan en 3-N friktionsstyrka motsatte sig rörelsen. Nu skulle frikroppsdiagrammet innehålla en 5-N-pil till höger och en 3-N-pil till vänster.

(bild 2)

Slutligen, anta att samma bok fanns på en lutning, glider ner. I detta scenario är de tre krafterna gravitationskraften i boken, som pekar rakt ner; normalkraften på boken, som pekar vinkelrätt mot ytan; och friktionskraften, som pekar motsatt rörelseriktningen.

(bild 3)
Beräkning av nettokraft |

När du har ritat frikroppsdiagrammet kan du använda vektortillägg att hitta nettokraften som verkar på föremålet. Vi kommer att överväga tre fall när vi utforskar denna idé:

Fall 1: Alla krafter ligger på samma linje.

Om alla krafter ligger på samma linje (pekar bara åt vänster och höger , eller bara upp och ned, till exempel, att bestämma nettokraften är lika enkel som att lägga till krafterna i positiv riktning och dra av krafterna i negativ riktning. (Om två krafter är lika och motsatta, som är fallet med boken som vilar på bordet, nettokraften \u003d 0)

Exempel: Tänk på en 1 kg boll som faller på grund av tyngdkraften och upplever en luftmotstånd kraft på 5 N. Det finns en nedåtriktad kraft på grund av tyngdkraften på 1 kg × 9,8 m /s ^{2 \u003d 9,8 N, och en uppåtkraft på 5 N. Om vi använder konventionen att upp är positiv, då nettokraften är 5 N - 9,8 N \u003d -4,8 N, vilket indikerar en nettokraft på 4,8 N i nedåtgående riktning.}

(bild 4)

Fall 2: Alla krafter ligger vinkelrätt axlar och lägg till 0 längs en axel.

I detta fall, på grund av krafter som lägger till 0 i en riktning, behöver vi bara fokusera på den vinkelräta riktningen när vi bestämmer nettokraften. (Även om kunskap om att krafterna i den första riktningen lägger till 0 kan ibland ge oss information om krafterna i vinkelrätt riktning, till exempel när man fastställer friktionskrafter i termer av den normala kraftstorleken.)

Exempel: A 0,25 kg leksaksbil skjuts över golvet med en 3-N kraft som verkar till höger. En 2-N friktionskraft agerar för att motsätta sig denna rörelse. Observera att tyngdkraften också verkar nedåt på denna bil med en kraft på 0,25 kg × 9,8 m /s ^{2 \u003d 2,45 N, och en normal kraft verkar uppåt, även med 2,45 N. (Hur vet vi detta? Eftersom det inte sker någon förändring i rörelse i vertikal riktning när bilen skjuts över golvet måste följaktligen nettokraften i den vertikala riktningen vara 0.)
Detta gör allt förenklat med det endimensionella fallet eftersom de enda krafterna som inte avbryter är längs en riktning. Nettokraften på bilen är då 3 N - 2 N \u003d 1 N till höger.}

(bild 5)

Fall 3: Alla krafter är inte begränsade till en linje och gör inte ligga på vinkelräta axlar.

Om vi vet i vilken riktning accelerationen kommer att vara, väljer vi ett koordinatsystem där den riktningen ligger på den positiva x-axeln eller den positiva y-axeln. Därifrån bryter vi varje kraftvektor i x- och y-komponenter. Eftersom rörelse i en riktning är konstant måste summan av krafterna i den riktningen vara 0. Krafterna i den andra riktningen är då de enda bidragsgivarna till nettokraften och detta fall har minskat till fall 2.

Om vi inte vet i vilken riktning accelerationen kommer att gå, kan vi välja vilket kartesiskt koordinatsystem som helst, även om det vanligtvis är mest bekvämt att välja en i vilken en eller flera av krafterna ligger på en axel. Bryt varje kraftvektor i x- och y-komponenter. Bestäm nettokraften i x
-riktningen och nettokraften i y
-riktningen separat. Resultatet ger x- och y-koordinaterna för nettokraften.

Exempel: En bil med 0,25 kg rullar utan friktion ner en 30-graders lutning på grund av tyngdkraften.

Vi kommer att använda ett koordinatsystem i linje med rampen som visas. Frikroppsdiagrammet består av tyngdkraften som verkar rakt ner och normalkraften verkar vinkelrätt mot ytan.

Vi måste bryta gravitationskraften in till x- och y-komponenter, vilket ger:
F_ { gx} \u003d F_g \\ sin (\\ theta) \\\\ F_ {gy} \u003d F_g \\ cos (\\ theta)

Eftersom rörelse i y-riktningen är konstant, vet vi att nettokraften i y-riktning måste vara 0:
F_N - F_ {gy} \u003d 0

(Obs: Denna ekvation tillåter oss att bestämma storleken på normalkraften.)

I x-riktningen är den enda kraften F _{gx
, följaktligen:
F_ {net} \u003d F_ {gx} \u003d F_g \\ sin (\\ theta) \u003d mg \\ sin (\\ theta) \u003d 0.25 \\ times9.8 \\ times \\ sin (30) \u003d 1.23 \\ text {N} Hur man hittar acceleration från nettokraft |}

När du har bestämt din nettokraftsvektor, hitta acceleration av ett objekt är en enkel tillämpning av Newtons andra lag.
\\ bold {F_ {net}} \u003d m \\ bold {a} \\ implicerar \\ bold {a} \u003d \\ frac {\\ bold {F_ {net}} } {m}

I det föregående exemplet på 0,25 kg-bilen som rullar ner ramp, nettokraften var 1,23 N ner rampen, så accelerationen skulle vara:
\\ bold {a} \u003d \\ frac {\\ bold {F_ {net}}} {m} \u003d \\ frac {1.23} {0.25 } \u003d 4,92 \\ text {m /s} ^ 2 \\ text {ner rampen}