
Reverse engineering beräkningsorigami för konform lindning. (A) Rynkor bildas när ett rektangulärt pappersark lindas tätt runt en Gaussisk yta som inte är noll. (B) Fraktalsnittsmönster kan undvika rynkor men oundvikligen leda till öppningar och oskyddade områden. (C) 2D-utvecklingen av en sfärisk polyeder som genereras automatiskt av beräkningsorigami kan linda en stålkula utan att lämna obetäckta områden. (D) När antalet fasetter ökar, nätets jämnhet och formbarhet förbättras naturligt. Skillnaden i ytarea mellan den perfekta sfären och den approximerade polyedern minskar med 5,3% när antalet fasetter ökar från 80 till 500. Hausdorff -avståndet mellan polyhedrala ytor och den perfekta sfären minskar också från 7,05 till 1,17% av radien för den perfekta sfären när antalet fasetter ökar från 80 till 500 (Foto:Y.-K. Lee, Seouls nationella universitet). Kredit:Science Advances, doi:10.1126/sciadv.aax6212
Den kontraintuitiva frågan om hur man lindar en krökt sfärisk yta med konventionellt styva och icke-töjbara eller spröda material, ligger till grund för denna studie. För att svara på frågan, Yu-Ki Lee och ett forskargrupp vid avdelningarna för materialteknik och datavetenskap i Republiken Korea och USA utökade en geometrisk designmetod för beräkningsorigami för att linda sfäriska konstruktioner i en ny rapport som nu publicerades i Vetenskapens framsteg . Tillvägagångssättet gav en robust och pålitlig metod för att konstruera konforma anordningar för godtyckligt krökta ytor med hjälp av ett beräkningskonstruerat icke-polyedriskt framkallbart nät. Den datorstödda designen omvandlade tvådimensionella (2-D) material som kisel (Si) skivor och stålplåtar till konforma strukturer som helt kunde omsluta 3D-strukturer utan sprickor eller deformation. Beräkningsmetoden för inslagning tillät dem att utveckla en designplattform för att omvandla konventionellt icke-töjbara 2-D-enheter till konforma 3-D-krökta ytor.
Studien introducerade en universell metod för konventionella icke-töjbara material för att linda in godtyckliga och olika 3-D böjda ytor genom att konstruera konforma materialenheter utan att offra deras prestanda. Till exempel, att slå in en sfär med ett rektangulärt papper kan oundvikligen bilda rynkor, Om man försöker slå in en sfär med ett segare underlag kan det leda till att omslagsmaterialet spricker. För att underlätta processen, materialforskare kan introducera mönstrade snitt i de icke-töjbara materialen, inklusive gitterskurna mönster och fraktala skärmönster för att effektivt linda in 3D-ytor. Sådana koncept är formprogrammerbara och kan effektivt täcka en sfär. Ingenjörer har också rekommenderat datoralgoritmer för att designa komplexa 3D-modeller baserade på 2D auxetiska strukturer. För att uppnå optimal täckning, de introducerade en beräkningsdesignstrategi känd som "beräkningsinpackning med icke-polyedriska utvecklingsbara nät, " för att forma icke-töjbara materialplattformar för wearables och konforma enheter.
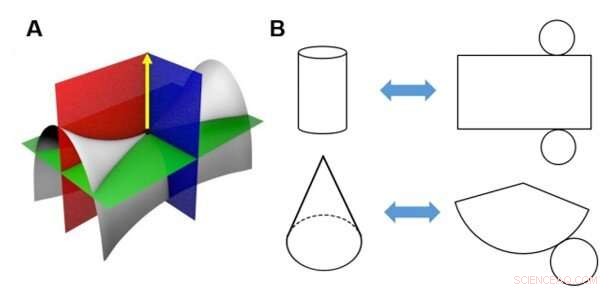
Matematisk begränsning av att linda ett plant ark runt en 3D -yta med icke -noll gaussiska krökningar. (A) Gaussisk krökning är vektorprodukten av de maximala och minsta huvudsakliga krökningarna vid en punkt. Vid sadelpunkten (svart punkt) på den grå ytan, en av de viktigaste krökningarna är skärningspunkten mellan de röda och gråa ytorna, och den andra är skärningspunkten mellan de blå och grå ytorna. Både det röda och blåa planet innehåller normalvektorn för sadelpunkten, och deras skärningar med den grå ytan definierar de huvudsakliga krökningarna. Ett 2D-material med noll gaussiska krökningspunkter, som ett pappersark, kallas en "utvecklabar yta", som inte kan omvandlas till en 3D-yta med en positiv eller negativ Gaussisk krökning (dvs. en "icke utvecklingsbar yta") utan att töjas eller komprimeras. (B) Till exempel, en cylinder eller en kon kan täckas med klippt papper, men en sadel eller en sfär kan inte lindas utan att det bildas rynkor eller skärsår. Den omvända (tillplattade) processen är också densamma, det är därför det finns snedvridningar i jordens plana karta. Kredit:Science Advances, doi:10.1126/sciadv.aax6212
I teorin, forskare kan karakterisera en krökt yta genom den Gaussiska krökningen – som är vektorprodukten av de maximala och minimala huvudkrökningarna vid en punkt. Till exempel, ett pappersark kallas en "framkallbar yta" och representerar ett 2D-material med noll Gaussisk krökning på alla punkter. En framkallningsbar yta kan inte förvandlas till en icke-utvecklabar 3D-yta utan att rivas, sträcka eller komprimera materialet. Konceptet är matematiskt bevisat av "Gauss Theorema Egregium, " som säger att "För att flytta en yta till en annan yta måste den Gaussiska krökningen för alla motsvarande punkter matcha." Datavetare har utövat stora ansträngningar för att algoritmiskt bestämma ytsnitt som segmenterar en icke-utvecklabar yta till framkallbara ytfläckar som kallas polyedriska nät eller helt enkelt - Nya beräkningsmetoder syftar till att optimera nätkvaliteten och vikbarheten med hjälp av maskininlärningsmetoder för att minska den tid och ansträngning som krävs för traditionella försök och felmetoder.
Eftersom de flesta verkliga 3D-objekt är jämna och krökta, forskare kräver högupplösta maskor för att täcka ytorna exakt. I det här arbetet, Lee et al. utvecklat ett nytt tillvägagångssätt som kallas "beräkningsinpackning" som går utöver den konventionella beräkningsvikningsmetoden. För att åstadkomma detta, de ansåg konform enhetsdesign som ett pappersomslagsproblem istället för en utmaning för pappersvikning (origami). Teamet kände igen funktionerna för att fästa och linda in konforma enheter för att täcka en underliggande böjd 3D-yta, helt enkelt genom att böja och pressa ett polyedriskt nät utan veck.

Koncept och fysisk demonstration av beräkningsinpackning. (A) När summan av vikningsvinklarna för ett nät minimeras, vecklinjerna kan ignoreras för att rymma flexibla men icke-töjbara styva och spröda material. För 500 mesh, mellanrummen i fallet med ett styvt material och rynkorna i fallet med ett flexibelt material är inte längre synliga, och skillnaden mellan de två blir omärklig. (B) En icke -töjbar plåt i rostfritt stål skärs i ett utvecklingsbart nät. (C) Med ett tillräckligt antal maskor, den rostfria stålplåten kan böjas och helt linda en sfär utan att skrynklas eller vikas. (D) En del av sfären är utfälld med 400 maskor, och vecklinjerna tas bort. (E) En 20 μm tjock spröd Si-wafer skärs till ett ovikt nät med en laserskärare. (F) Den skurna Si-skivan omsluter stabilt både konvexa och konkava ramar. (Fotokredit:Y.-K. Lee, Seouls nationella universitet). Kredit:Science Advances, doi:10.1126/sciadv.aax6212
Högupplösta maskor gjorde det möjligt för dem att ta itu med gränserna för långa tillverkningstider och mekanisk tillförlitlighet. För att innesluta en yta med en rund Gaussisk krökning som inte är noll, som en perfekt sfär, Lee et al. använde en framkallningsbar yta efter att ha förfinat facettnätet för att möta de erforderliga värdena för inpackningstäthet. Resultaten gav data om ett icke -polyhedralt utvecklingsbart nät för att skapa kontrollerade och bundna utrymmen mellan nätet och sfären utan luckor eller överlappningar mellan fasetterna. Tillverkningsprocessen producerade noggrant mycket komplexa och släta 3D-ytor många gånger snabbare än konventionella beräkningsmetoder för vikning vid hantering av komplexa former med papper, metalliska och keramiska förpackningsmaterial. Finita elementanalys stödde att sådana beräkningsförpackningar var mekaniskt tillförlitliga.

Finita element (FE) simulering för att linda en sfär med en 100 µm tjock Si-wafer med ett icke-polyedriskt framkallbart nät. Kredit:Science Advances, doi:10.1126/sciadv.aax6212
De strukturer som utvecklades i arbetet ledde till en betydande ökning av beräkningsorigami för verkliga industriella tillverkningsprocesser. Till exempel, Lee et al. utvecklat en konform enhet med elektroluminescerande lampa (EL) paneler för att linda en sfär, den resulterande 3-D konforma enheten uppvisade bra funktion och de krediterade resultaten till böjnings- och pressprocesser som användes för att linda sfären istället för vecknings- och vikningstekniker. Teamet demonstrerade också sin metod på en kommersiell koreansk mask och på ett elektriskt leksaksfordon med fastsatta EL -paneler för att fungera utan att misslyckas. Att generera det utvecklingsbara nätet för komponenter med Gauss-ytor som inte är noll, såsom strålkastarna på det elektriska leksaksfordonet, forskarna använde den genetiska algoritmen (GA) utvecklingsmetoden.

Demonstration av konforma anordningar. (A) Klippbar, icke töjbar, kommersiella EL-paneler som består av spröda elektroder skärs med en laserskärare för att bilda framkallbara nät för en sfär. (B) EL-paneler med ett framkallbart nät kan helt täcka en sfär och (C) fungera utan katastrofala fel. (D och E) Det beräkningsmässiga omslagskonceptet demonstreras också för en ellipsoidmodell. (F och G) Förutom en sfär och en ellipsoid, en kommersiell koreansk ansiktsmask kan också täckas med EL-paneler och användas utan elfel. (H) Ett elektriskt leksaksfordon kan också lindas med EL-paneler på samma sätt, och de bifogade EL-panelerna fungerar också bra utan fel. Utvecklingsmetoden GA används för att generera det utvecklingsbara nätet för delar med Gauss -ytor utan noll, inklusive (I) strålkastarna, kanten på den främre sidostötfångaren, och (J) kanten på den bakre sidofångaren på det elektriska leksaksfordonet. (Fotokredit:Y.-K. Lee, Seoul National University.) Kredit:Science Advances, doi:10.1126/sciadv.aax6212
På det här sättet, Yu-Ki Lee och kollegor introducerade konceptet med beräkningsinpackning för att konvertera icke-töjbara 2D-flexibla enheter till 3D-konforma enheter. Med hjälp av metoden, de innesluten en yta med icke-noll Gaussisk krökning såsom en perfekt sfär. Den föreslagna tekniken skulle kunna styra avståndet mellan de två ytorna för att säkerställa tät omlindning. Verket producerade en enda ansluten yta känd som ett icke-polyedriskt framkallbart nät, utformad för att linda in ett 2D-ark för alla 3D-ytor. Som ett resultat, forskarna kunde till och med underlätta för styva och spröda material som metallplåtar och Si-wafers för att helt täcka och linda in Gaussiska krökningsytor som inte var noll. Den universella beräkningsmetoden som utvecklats i detta arbete kommer att ge nya insikter i utvecklingen av konforma enheter med godtyckliga former med hjälp av effektiva algoritmer och robusta, pålitliga tillverkningsmetoder.
© 2020 Science X Network