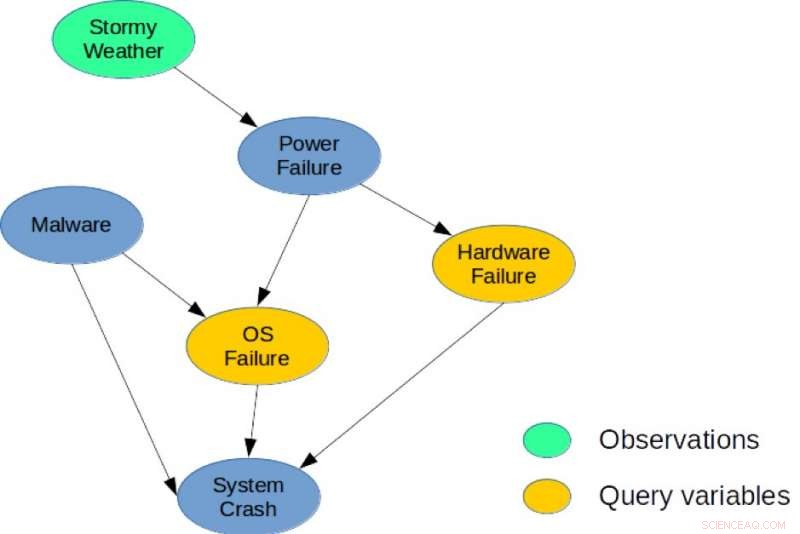
Figur 1. Ett enkelt Bayesiskt nätverk för en systemdiagnosuppgift. Kredit:IBM
Det finns ett djupt samband mellan planering och slutsatser, och under det senaste decenniet, flera forskare har infört explicita minskningar som visar hur stokastisk planering kan lösas med hjälp av probabilistisk slutledning med tillämpningar inom robotik, schemaläggning, och miljöproblem. Dock, heuristiska metoder och sökning är fortfarande de bästa metoderna för planering i stora kombinatoriska tillstånd och handlingsutrymmen. Mina medförfattare och jag tar ett nytt tillvägagångssätt i vårt papper, "Från Stokastisk planering till Marginal MAP" (författare:Hao Cui, Radu Marinescu, Roni Khardon), vid 2018 Conference on Neural Information Processing Systems (NeurIPS) genom att visa hur idéer från planering kan användas för slutsatser.
Vi utvecklade Algebraic Gradient-based Solver (AGS), en ny lösare för ungefärliga marginella MAP -slutsatser. Algoritmen bygger en ungefärlig algebraisk beräkningsgraf som fångar tillståndsmarginaler och belöningsvariabler under oberoende antaganden. Den använder sedan automatisk differentiering och gradientbaserad sökning för att optimera val av åtgärder. Vår analys visar att värdet som beräknas av AGS-beräkningsgrafen är identiskt med lösningen av Belief Propagation (BP) när det är betingat av handlingar. Detta ger en tydlig koppling mellan heuristiska planeringsalgoritmer och ungefärlig slutsats.
Mer specifikt, vi återbesöker sambandet mellan stokastisk planering och sannolikhetsslutning. Vi föreslår för första gången att använda en effektiv heuristisk algoritm som ursprungligen designades för att lösa planeringsproblem för att ta itu med en central slutledningsuppgift för probabilistiska grafiska modeller, nämligen uppgiften marginell maximal a posteriori sannolikhet (MMAP).
Probabilistiska grafiska modeller som Bayesianska nätverk eller Markov-nätverk ger ett mycket kraftfullt ramverk för resonemang om villkorliga beroendestrukturer över många variabler. För sådana modeller, MMAP -slutsatsfrågan är en särskilt svår men ändå viktig uppgift, motsvarande att hitta den mest troliga konfigurationen (eller maximera sannolikheten) över en delmängd av variabler, kallas MAP-variabler, efter att ha marginaliserat (eller summerat) resten av modellen.
MMAP -slutsats uppstår i många situationer, speciellt vid diagnos- och planeringsuppgifter, där den mest naturliga specifikationen av modellen innehåller många variabler vars värden vi inte bryr oss om att förutsäga, men som skapar ömsesidigt beroende mellan variablerna av intresse. Till exempel, i en modellbaserad diagnosuppgift, givna observationer, vi försöker optimera över en undergrupp av diagnosvariabler som representerar potentiellt felaktiga komponenter i ett system.
Till illustration, betrakta det bayesianska nätverket som visas i figur 1, som skildrar ett enkelt diagnosproblem för ett datorsystem. Modellen fångar direkta kausala beroenden mellan sex slumpvariabler som används för att beskriva detta problem. Specifikt, en systemkrasch kan orsakas av ett maskinvarufel, ett OS-fel, eller förekomsten av skadlig programvara i systemet. Liknande, ett strömavbrott kan vara en vanlig orsak till maskinvaru- och OS-fel, och stormigt väder kan orsaka strömavbrott. En möjlig MMAP-fråga skulle vara att beräkna den mest sannolika konfigurationen av maskinvaru- och OS-fel, med tanke på att vi observerar Stormy Weather, oavsett tillståndet för de andra variablerna (Malware, Systemkrasch, eller strömavbrott).
Stokastiska planeringsramar som Markov -beslutsprocesser används i stor utsträckning för att modellera och lösa planeringsuppgifter under osäkerhetsförhållanden. Planering med ändlig horisont kan fångas med hjälp av ett dynamiskt Bayesian-nätverk (DBN) där tillstånds- och åtgärdsvariabler vid varje tidssteg representeras explicit och de villkorade sannolikhetsfördelningarna av variabler ges av övergångssannolikheterna. I offlineplanering, uppgiften är att beräkna en policy som optimerar den långsiktiga belöningen. I kontrast, i on-line planering får vi en fast begränsad tid t per steg och kan inte beräkna en policy i förväg. Istället, med tanke på det nuvarande läget, Algoritmen måste besluta om nästa åtgärd inom tid t. Sedan utförs åtgärden, en övergång och belöning observeras och algoritmen presenteras med nästa tillstånd. Denna process upprepas och algoritmens långsiktiga prestanda utvärderas.
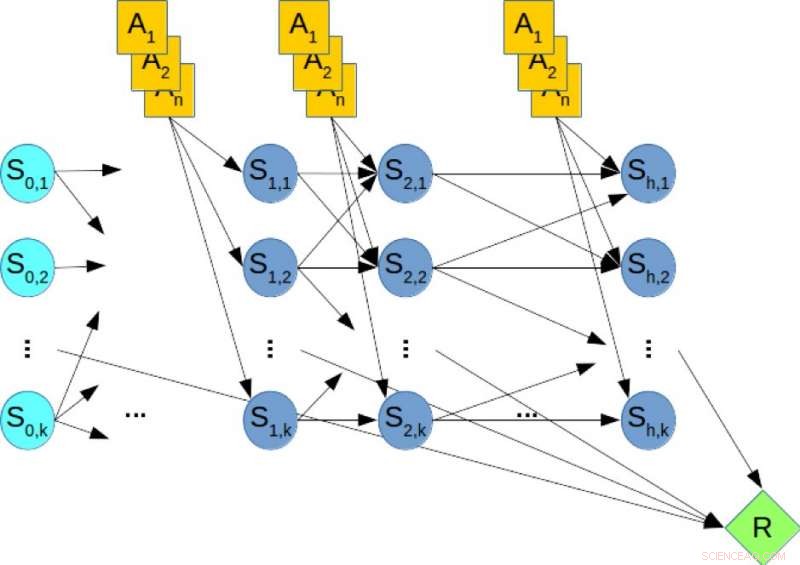
Figur 2. Ett dynamiskt bayesiskt nätverk (DBN) för stokastisk planering. Kredit:IBM
Till illustration, betrakta figur 2, som visar DBN som motsvarar ett hypotetiskt planeringsproblem, där de orangea noderna representerar åtgärdsvariablerna, de blå noderna anger tillståndsvariablerna, och den gröna noden anger den kumulativa belöningen som måste maximeras. Därför, att beräkna den optimala policyn för planeringsproblemet motsvarar att lösa en MMAP-fråga över DBN, där vi maximerar över åtgärdsvariablerna och marginaliserar tillståndsvariablerna.
Vår experimentella utvärdering av svåra MMAP-probleminstanser visar definitivt att AGS-schemat förbättras jämfört med prestandan när som helst för toppmoderna algoritmer på MMAP-problem med hårda summeringssubproblem, ibland med upp till en storleksordning. Vi tror att dessa samband mellan planering och slutledning kan utforskas ytterligare för att ge förbättringar inom båda områdena.
Den här historien återpubliceras med tillstånd av IBM Research. Läs originalberättelsen här.