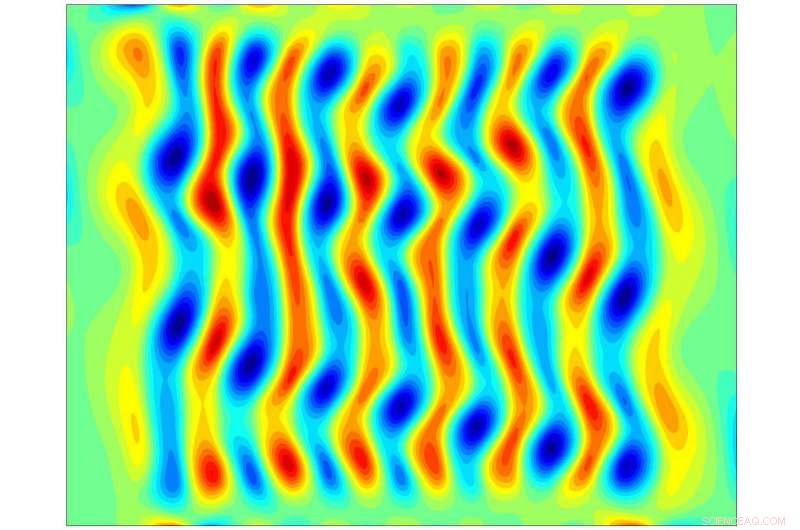
En analyserad ögonblicksbild av ett ögonblick av turbulent flöde, I detta fall, en exakt koherent struktur (ECS). Upphovsman:Georgia Tech / Schatz / Grigoriev
Ett gammalt ordspråk säger att en fjärilsvinges flik i Brasilien kan utlösa en tornado i Texas veckor senare. Även om kaosteorin säger att det i princip är omöjligt att beräkna exakt hur det kan hända, forskare har gjort framsteg med att tillämpa matematik för att förutsäga fenomenet bakom det som kallas turbulens.
De senaste framstegen från fysiker från Georgia Institute of Technology kan en dag hjälpa till att vässa väderprognoser och utöka sitt intervall genom att bättre använda massor av väder- och klimatdata.
Turbulens kan kurva som ett luftpust, virvla förbi en flodböjning eller svänga som en orkan, och även om dess curlicues kan verka slumpmässiga, turbulens fastställer signaturmönster som fysikerna undersöker. De har utvecklat en enkel matematisk modell som har hjälpt dem att visa hur turbulenta flöden kommer att utvecklas över intervaller.
Och, i ett nytt experiment, de verifierade sina förutsägelser fysiskt i ett tvådimensionellt turbulent flöde producerat i ett labb.
”Butterfly Effect” -fras
Den nya Georgia Tech -forskningen passar uppfattningen till detta ordspråk.
Det myntades för mer än 55 år sedan av MIT meteorologiprofessor Edward Lorenz efter att han konstaterade att små krafter påverkade stort väder tillräckligt för att kasta långdistansprognoser för en slinga. Titeln på hans tidning, "Förutsägbarhet:Utlöser en fjärilsvinge i Brasilien en tornado i Texas?" förvandlats till det välkända slagordet.
Michael Schatz och Roman Grigoriev, professorer i Georgia Tech's School of Physics, tillsammans med forskare Balachandra Suri och Jeffrey Tithof, publicerade sina forskningsresultat online i tidskriften Fysiska granskningsbrev onsdagen den 15 mars, 2017. Forskningen finansierades av National Science Foundation.
Ordning i kaos
I hundratals år, medan forskare använde matte för att få grepp om Newtons fallande äpple, underbygga relativitetsteorin och teoretisera existensen av Higgs boson, turbulens har varit som våt tvål i matematikens grepp. Men för all sin svårfånglighet, turbulens imponerar med synligt sammanhängande, återkommande, igenkännbara former.
Vätskvirvlar etablerar sig snabbt och skiftar eller försvinner, men de återkommer ihållande på olika platser, producerar övergående och varierande, men upprepar mönster.
"Människor har sett dessa mönster i turbulenta flöden i århundraden, men vi hittar sätt att relatera mönstren till matematiska ekvationer som beskriver vätskeflöden, "Sa Grigoriev. Några återkommande mönster, särskilt, intresse Grigoriev och Schatz. De kallas exakta koherenta strukturer (ECS).
De ger fysikerna praktiska ingångspunkter till beräkningsprognoser om vad turbulens kommer att göra härnäst.
Turbulenta flödesbilder
Men vad är dessa exakta sammanhängande strukturer? Visuellt, i turbulens, de kan dyka upp som flyktiga ögonblick när mönstren slutar förändras. Och det kan se ut som att flödet bromsar tillfälligt.
För det otränade ögat, en ECS ser inte mycket annorlunda ut än resten av virvlarna och lockarna, men man kan lära sig att upptäcka dem. "Det är precis så vi går tillväga för att hitta dem, " sa Schatz. "Vi tittar på turbulensen, ständigt ta ögonblicksbilder. Flödet rör sig, flyttar runt. Vi letar efter det ögonblick då det saktar ner som mest, och vi tar en ögonblicksbild. "
"Vi matar det in i den matematiska modellen, "Sa Schatz, "och det indikerar att vi är nära, och visar hur matematiken ser ut vid den punkten. "Den matematiska lösningen beskriver en punkt i det turbulenta flödet som kan arbetas med för att beräkna en förutsägelse om vad turbulensen kommer att göra nästa.
För att förstå vad en exakt koherent struktur är dynamiskt, vi måste ta ett steg tillbaka från hur turbulens ser ut visuellt med knippen av lockar och virvlar. Istället, låt oss titta på ett turbulent flöde som en enda fysisk enhet genom att översätta det till en rå metafor, en svängande pendel - med några märkliga konstigheter.
Pendel på huvudet
Det här kommer att bli lite abstrakt:Först, vänd på pendeln.
Istället för att föreställa sig bottenpunkten på en normal pendels sving, jämvikten, som en stabil punkt i en stabil sväng, nu, med den uppochnedvända pendeln, jämvikten är den högsta punkten. Och det är instabilt. Också, den svänger inte åt bara två håll utan i alla riktningar.
Ett turbulent flödes tillförlitliga mönster speglar dynamik som är fram och tillbaka-till-och-tillbaka men i alla möjliga variationer.
När den metaforiska pendeln svänger upp mot sin topp, det kommer till ett nära men aldrig helt stopp. Istället floppar det över till någon annan sida. Den nära stopppunkten är analog med en exakt koherent struktur, men det finns några fler knäck i metaforen.
"Om vi ändrar initial dynamik så lite, en omvänd pendel kan svänga förbi sin instabila jämvikt vid toppen, eller det kan stanna och sedan börja röra sig i motsatt riktning. På samma sätt, det turbulenta flödet kan utvecklas på olika sätt efter att ha passerat ett ECS, Sa Grigorjev.
Flera exakt sammanhängande strukturer med varierande kvaliteter dyker upp i ett turbulent flöde.
Turbulensvägar till ECS-städer
Att alla kan kännas ovanliga av en anledning.
"Vanligtvis, människor gillar att titta på stabila saker som är oförändrade som jämna, symmetrisk normal pendel, "Schatz sa." Det visar sig att det verkligen är dessa instabila mönster som bildar ett grovt kärnalfabet som vi använder för att bygga en slags förutsägande teori. "
Håller på med dynamiken i den diskett inverterade pendeln, föreställ dig nu varje exakt sammanhängande struktur som en stad på en karta. Det finns vägar som styr det turbulenta flödet "trafik" mot, från, och runt varje stad precis som vägar. "Denna vägkarta runt och mellan städer förändras inte i tid, vilket gör att vi kan förutsäga flödets utveckling, Sa Grigorjev.
ECS förekommer regelbundet, nästan som urverk, öppnar upp för möjligheten att förfina förutsägelser med jämna mellanrum.
Exakta sammanhängande strukturer var redan kända för att existera, Sa Schatz. "Vad ingen har gjort tidigare är att demonstrera i ett labbexperiment hur de kan utnyttjas för att beskriva dynamik, beteendet utvecklas i tid, vilket verkligen är vad du behöver för att förutsäga."
Väderdata för gruvdrift
På 1800-talet, matematiska ekvationer utvecklades för att beskriva det grundläggande flödet av vätskor. De som tog gymnasiefysik kan komma ihåg Newtons andra lag om krafter, acceleration och massa. Navier-Stokes ekvationer, används i denna studie, applicera det på vätskor.
Turbulens är utmanande att beskriva matematiskt eftersom dess virvlar innehåller otaliga dimensioner, med flödet i varje liten region som verkar dansa till sin egen melodi. Men det finns en tydlig ordning som uppstår när man hittar exakta sammanhängande strukturer.
För att göra sina förutsägelser, Schatz och Grigorievs forskargrupp utarbetade ett sätt att matematiskt koppla den höga dimensionen till det mycket enklare vägbanekonceptet.
De bryter ner det turbulenta flödet till regioner, var och en tillräckligt liten för att tillämpa ekvationerna, använde sedan sina lösningar för att exakt placera flödena på färdplanen.
I dag, data över väder och klimat, formen på havsbotten, atmosfärens dimensioner, tyngdkraftens effekter, rotation, eller koncentrationer av lösta mineraler är imponerande och växande.
Prediktiva metoder som de i denna forskning erbjuder vägar in i denna data för att extrahera bättre förutsägelser från den.