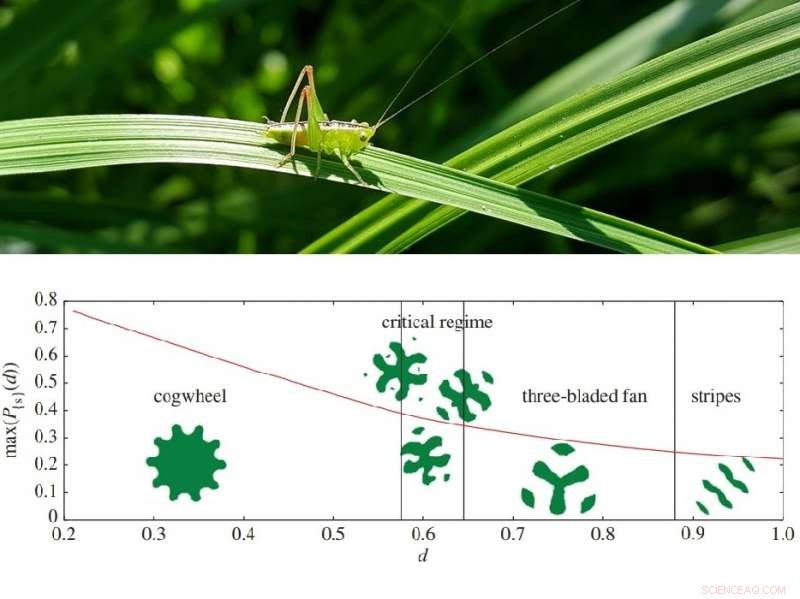
Några av de optimala gräsmattsformerna, som beror på avståndet gräshoppan hoppar. Bortom den kritiska regimen, de bästa konfigurationerna kopplas bort. Diagramkredit:Goulko et al. Royal Society. Kredit:Pixabay.
(Phys.org) – Liksom många matematiska pussel, gräshoppaproblemet är enkelt att ange men svårt att lösa:en gräshoppa landar på en slumpmässig punkt på en gräsmatta i område 1, hoppar sedan en gång, ett fast avstånd, i en slumpmässig riktning. Vilken form ska gräsmattan ha för att maximera chansen att gräshoppan stannar kvar på gräsmattan efter att ha hoppat?
Ett första intryck kan vara att gräsmattan ska vara i form av en cirkel, åtminstone när avståndet som gräshoppan hoppar är litet. Dock, Olga Goulko och Adrian Kent, de två fysikerna som introducerade gräshoppsproblemet i en ny tidning, har matematiskt bevisat att en skivformad gräsmatta inte är optimal för alla avstånd.
Istället, de upptäckte genom numeriska simuleringar att den optimala gräsmattans form antar en mängd olika komplexa former för olika hoppavstånd, såsom en kugghjulsform för avstånd mindre än 1/π 1/2 (radien för en cirkel med area 1, eller ungefär 0,56), medan för större avstånd, den optimala gräsmattan består av frånkopplade bitar. Ofta, men inte alltid, dessa optimala former har någon typ av symmetri.
Motiverad av fysik
Förutom att det är ett intressant geometriproblem, gräshoppaproblemet är också nära relaterat till forskning inom kvantfysik och kan ha en mängd olika tekniska tillämpningar. Särskilt, gräshoppaproblemet är kopplat till Bell-ojämlikheterna, som berömt visar att, till skillnad från klassiska fysikmodeller, kvantteorin lyder inte lokal realism. Ett utmärkt exempel på kränkningen av lokal realism ses i kvantintrassling, där två avlägsna intrasslade system uppvisar korrelationer som inte kan förklaras av någon modell som lyder lokal realism.
Denna koppling till Bell-ojämlikheterna är, faktiskt, vad som ursprungligen motiverade Goulko och Kent att föreslå gräshoppaproblemet. Ett öppet problem inom fysiken när det gäller Bell-ojämlikheterna är att bestämma de optimala gränserna som bryts av kvantteorin när kvantkorrelationer mäts på en sfär i vinklar mellan 0 och 90 grader. Det visar sig att detta problem med att bestämma de optimala gränserna är ekvivalent med problemet med att bestämma gräshoppsproblemets gräsmattaform när gräsmattan är sfärisk snarare än platt mark. I den sfäriska versionen av gräshoppeproblemet, avståndet som gräshoppan hoppar över plan mark ersätts av vinkeln med vilken den hoppar över sfären.
I deras papper, som publiceras i ett färskt nummer av Proceedings of The Royal Society A , Goulko och Kent har bara analyserat den plana versionen av gräshoppsproblemet, även om de förväntar sig att det inte borde vara för svårt att tillämpa samma numeriska tekniker på det sfäriska fallet. Sedan, när man tar hänsyn till några ytterligare begränsningar, det kan vara möjligt att äntligen lösa problemet med optimala gränser för Bell-ojämlikheterna.
"Vi planerar att gå vidare till arbetet med de sfäriska versionerna av gräshoppsproblemet som är relevanta för Bell-ojämlikheter, och förväntar oss att våra metoder ska fungera där, " berättade Kent Phys.org .
Ny gräns
Som fysikerna förklarar, en av de överraskande sakerna med gräshoppaproblemet är att inget liknande det någonsin har föreslagits tidigare. Även om grundidén är okomplicerad nog att problemet kunde ha ställts av den antika grekiske matematikern Euklid, som lade grunden till modern geometri, forskarna känner inte till någon tidigare version av problemet, antingen i antik eller modern tid.
"Det är trevligt att bli påmind om att även i ett fält så gammalt som geometri, man kan fortfarande hitta enkla nya frågor som har överraskande svar och öppnar upp för nya forskningslinjer, sa Kent.
Som ett helt nytt problem, det finns ett oändligt antal framtida forskningsriktningar att ta. Till exempel, fysikerna föreslår att gräshoppan får ta flera hopp, eller att kräva att gräshoppan går och stannar kvar på gräsmattan på alla punkter på dess väg (en variant som de kallar "myrproblemet"). Andra möjliga variationer inkluderar generalisering till högre dimensioner, analysera andra gräsytor än sfärer och plan, med tanke på en variant av problemet med två olika arter av gräsmattsfrön som kan överlappa varandra i samma region (vilket är särskilt relevant för Bell-ojämlikheter), och att lägga ytterligare begränsningar på möjliga lösningar.
Självklart, sådana frågor handlar egentligen inte om gräshoppor och gräsmattor, eftersom den underliggande strukturen erbjuder ett sätt att modellera olika verkliga situationer. Ett exempel som forskarna pekar på är kärnkedjereaktioner. I en kedjereaktion, en högenergipartikel påverkar en slumpmässig atomkärna, får den att genomgå klyvning, som producerar en annan högenergipartikel som färdas en viss sträcka för att träffa en annan slumpmässig kärna, och processen upprepas. Genom att modellera denna situation med gräshoppaproblemet, den optimala gräsytan motsvarar den maximala initiala reaktionshastigheten, vilket maximerar antalet kärnor som deltar i kedjereaktionen.
En annan potentiell tillämpning av gräshoppsproblemet ligger i modellering av kvantkommunikationsprotokoll, som forskarna förklarar kan ses som en gräshoppamodell där den ena parten måste välja vilken algoritm (gräsformen) som ska användas för att kommunicera med en andra part.
Och slutligen, forskarna föreslår att det kan vara intressant att undersöka ursprunget till själva gräsmattans former, eftersom vissa av gräsmattans mönster liknar mönster som upprepade gånger dyker upp i naturen, som i blommor, snäckskal, och djurränder. I enlighet med teorin om morfogenes som föreslagits av Alan Turing, dessa mönster kan uppstå som optimala lösningar av kemiska skäl, som kan hjälpa till att förklara de olika och komplexa formerna på gräsmattorna som förekommer i gräshoppsproblemet.
© 2017 Phys.org