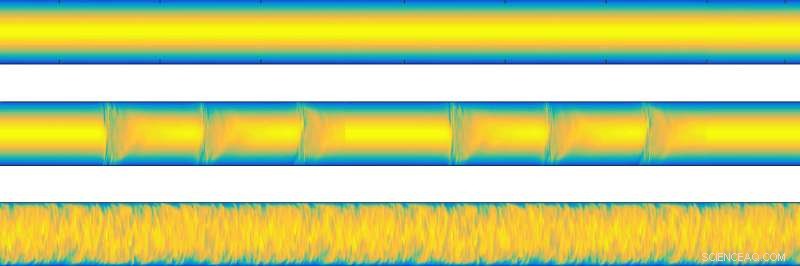
Olika typer av rörflöde. Uppifrån och ner:laminär, övergående och turbulent. Upphovsman:Okinawa Institute of Science and Technology
Oavsett om en vätska strömmar genom hushållens VVS eller industriella olje- och gasledningar, när den går långsamt är dess flöde jämnt, men när det går snabbt är dess flöde mer kaotiskt.
För mer än 130 år sedan, Den brittiska fysikern och ingenjören Osborne Reynolds beskrev vätska som flödar vid låga hastigheter som 'laminär, betyder att det flyter smidigt i en enda riktning, och vätska som flödar i höga hastigheter som 'turbulent, betyder att det upplever kaotiska förändringar i tryck och energi. Reynolds utvecklade en uppsättning ekvationer för att beskriva förhållandet mellan hastigheten med vilken en vätska flyter och friktionen som skapas mellan den och röret.
Ingenjörer använder fortfarande Reynolds "lagar av motstånd" idag för att beräkna hur mycket energi som går förlorad till friktion när vätskor och gaser strömmar genom ett rör. Dock, ett mysterium har förblivit olöst:vad händer när ett flöde övergår från laminärt till turbulent?
"I övergångsflödet, friktion varierar utan märkbara mönster, "säger Dr Rory Cerbus, en postdoktor vid Okinawa Institute of Science and Technology Graduate University (OIST). Tills nu, motståndets lagar för övergångsflöde var okända, vilket gör det svårt att beräkna friktion och energiförlust under denna typ av flöde.
En figur från Osborne Reynolds papper från 1883, visar Reynolds assistent som står bredvid apparater som används för att mäta friktion i olika typer av flöden. Upphovsman:Okinawa Institute of Science and Technology
Cerbus och andra forskare vid Fluid Mechanics Unit och Continuum Physics Unit vid OIST har hittat en förvånansvärt enkel lösning på denna 130 år gamla gåta. "Vi har visat att även om övergångstillståndet verkar vara en menageri av flödestillstånd, alla dessa kan kännetecknas av lagar som vi redan känner till, "säger professor Pinaki Chakraborty, chef för enheten för vätskemekanik. "Detta förenklar ett grundläggande problem."
Övergångsflöde är känt för att bestå av intermittenta fläckar av olika typer av flöden, som alternerar längs rörledningen. I standardmetoden för att mäta friktion i övergångsflöde, de är helt enkelt klumpade ihop.
OIST -forskarna analyserade istället fläckarna med jämnt och kaotiskt flöde separat. De sprang vatten genom ett 20-metersglasrör. Genom att tillsätta små partiklar till vattnet och belysa det med en laser, de kunde mäta flödets hastighet. Detta gjorde det möjligt för dem att rent identifiera de omväxlande fläckarna av jämnt och kaotiskt flöde i övergångsflödet. De mätte sedan friktionen inuti de enskilda fläckarna med hjälp av trycksensorer.
"Vi upprepade ett läroboksexperiment som rutinmässigt utförs av tusentals ingenjörer varje år över hela världen, "säger Cerbus, huvudförfattare till tidningen, som nyligen publicerades i Fysiska granskningsbrev . "Vi använde i princip samma verktyg, men med den avgörande skillnaden att analysera plåstren separat, " han säger.

Dr Rory Cerbus förklarar skillnaden mellan laminar, turbulent och övergångsflöde. Som hans diagram visar, övergångsflöde - den typ av flöde som forskarna studerat - har intermittenta fläckar av jämnt och kaotiskt flöde. Upphovsman:Okinawa Institute of Science and Technology
Forskarna visade att trots de yttre komplexiteten, motståndslagen för de släta fläckarna överensstämmer med laminärt flöde, medan motståndslagen för de kaotiska fläckarna överensstämmer med turbulent flöde. Därför, övergångsflöde kan studeras med hjälp av Reynolds ursprungliga motståndslagar.
Att förstå hur mycket energi som krävs för att pumpa vätska genom en rörledning när den flyter i övergångsläget kan hjälpa industrier, såsom oljeraffinaderier, minimera energislöseri och förbättra effektiviteten.
"Om du tittar noga, du upptäcker att det ofta finns enkelhet under komplexiteten, säger Chakraborty.