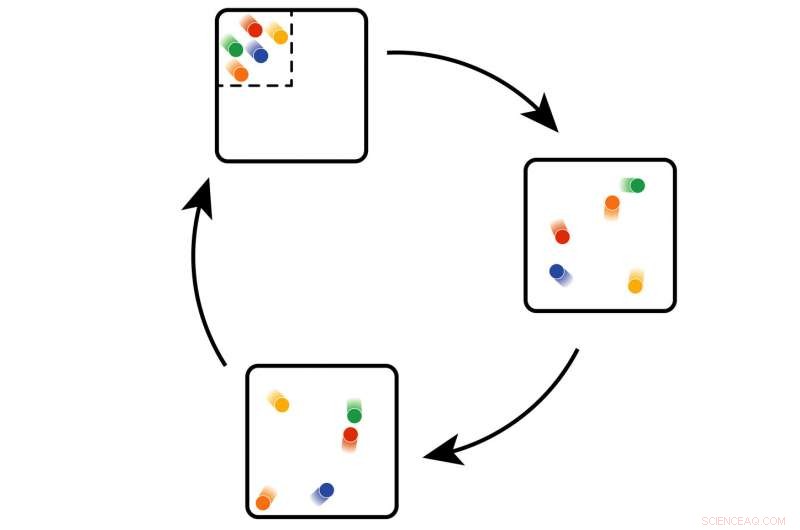
Återkommande kan demonstreras med bollar i en låda:när de börjar i ett beställt tillstånd, de kommer att bli mer oordning. Men någon gång, de kommer att återgå till utgångsläget - det kan bara ta ett tag. Upphovsman:TU Wien
Det är ett av de mest häpnadsväckande resultaten av fysiken - när ett komplext system lämnas ensamt, den kommer att återgå till sitt ursprungliga tillstånd med nästan perfekt precision. Gaspartiklar, till exempel, kaotiskt virvlar runt i en behållare, kommer att återvända nästan exakt till sina utgångslägen efter en tid. Poincaré Recurrence Theorem är grunden för modern kaosteori. I årtionden, forskare har undersökt hur denna sats kan tillämpas på kvantfysikens värld. Nu, forskare vid TU Wien (Wien) har framgångsrikt demonstrerat ett slags återkommande Poincaré i ett kvantsystem med flera partiklar. Resultaten har publicerats i tidningen Vetenskap .
I slutet av 1800 -talet, den franska forskaren Henri Poincaré studerade system som inte kan analyseras fullständigt med perfekt precision - till exempel solsystem bestående av många planeter och asteroider, eller gaspartiklar som fortsätter stöta på varandra. Hans överraskande resultat:Varje tillstånd som är fysiskt möjligt kommer att ockuperas av systemet någon gång - åtminstone till en mycket bra approximation. Om vi bara väntar tillräckligt länge, någon gång kommer alla planeter att bilda en rak linje, bara av en slump. Gaspartiklarna i en låda kommer att skapa intressanta mönster, eller gå tillbaka till det tillstånd där de var när experimentet startade.
En liknande sats kan bevisas för kvantsystem. Där, dock, helt andra regler gäller:"I kvantfysik, vi måste komma på ett helt nytt sätt att lösa detta problem, "säger professor Jörg Schmiedmayer från Institute for Atomic and Subatomic Physics vid TU Wien." Av mycket grundläggande skäl, tillståndet i ett stort kvantsystem, bestående av många partiklar, kan aldrig mätas perfekt. Förutom det, partiklarna kan inte ses som oberoende objekt, vi måste ta hänsyn till att de är kvantemekaniskt intrasslade. "

Atomchipet, används för att styra ultrakalla atommoln. Upphovsman:TU Wien
Det har gjorts försök att visa effekten av "Poincaré -återfall" i kvantsystem, men hittills har detta bara varit möjligt med ett mycket litet antal partiklar, vars tillstånd mättes så exakt som möjligt. Detta är extremt komplicerat och den tid det tar för systemet att återgå till sitt ursprungliga tillstånd ökar dramatiskt med antalet partiklar. Jörg Schmiedmayers team på TU Wien, dock, valde ett annat tillvägagångssätt:"Vi är inte så intresserade av systemets fullständiga inre tillstånd, som ändå inte kan mätas, "säger Bernhard Rauer, publikationens första författare. "I stället vill vi fråga:vilka mängder kan vi observera, som berättar något intressant om systemet som helhet? Och finns det tillfällen då dessa kollektiva kvantiteter återgår till sitt ursprungliga värde? "
Teamet studerade beteendet hos en ultrakyld gas, som består av tusentals atomer, som hålls på plats av elektromagnetiska fält på ett chip. "Det finns flera olika storheter som beskriver egenskaperna hos en sådan kvantgas - till exempel koherenslängder i gasen och korrelationsfunktioner mellan olika punkter i rymden. Dessa parametrar berättar för oss, hur nära partiklarna är länkade mellan kvantmekaniska effekter, säger Sebastian Erne, som var ansvarig för de teoretiska beräkningar som var nödvändiga för projektet. "Vår vardagliga intuition är inte van vid att hantera dessa mängder, men för ett kvantsystem, de är avgörande. "
Återkommande upptäckt - i kollektiva mängder
Genom att mäta sådana mängder, som inte avser enskilda partiklar, men kännetecknar systemet som helhet, det var verkligen möjligt att observera det efterlängtade kvantåterfallet. Och inte bara det:"Med vårt atomchip, vi kan till och med påverka den tid det tar för systemet att återgå till ett särskilt tillstånd, "säger Jörg Schmiedmayer." Genom att mäta denna typ av återkommande, vi lär oss mycket om atomernas kollektiva dynamik - till exempel om ljudets hastighet i gasen eller om spridning av fenomen i densitetsvågor. "
Den gamla frågan, om kvantsystem visar återfall, kan äntligen besvaras:Ja, de gör det - men begreppet återfall måste definieras något. Istället för att försöka kartlägga det fullständiga inre kvanttillståndet i ett system, som ändå inte kan mätas, det är mer meningsfullt att koncentrera sig på kvantiteter som kan mätas i kvantexperiment. Dessa mängder kan observeras att de försvinner från sitt ursprungliga värde - och så småningom återgår till sitt ursprungliga tillstånd.