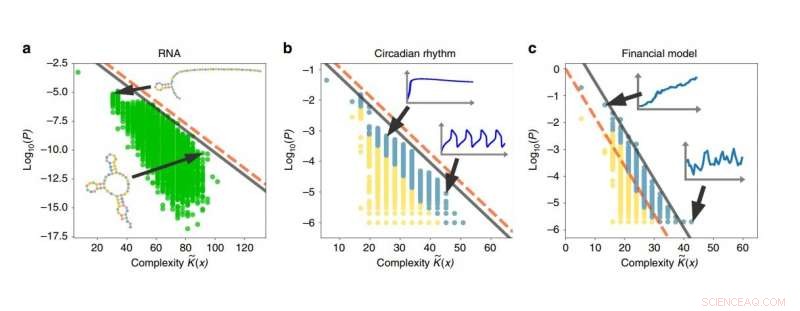
Exempel på enkelhetsfördom i RNA -sekvenser, dygnsrytmer, och finansiella modeller. Ju högre komplexitet en utgång är, desto lägre är sannolikheten att utmatningen genereras. Upphovsman:Dingle, et al. Publicerad i Naturkommunikation
Forskare har upptäckt att input-output-kartor, som används mycket inom vetenskap och teknik för att modellera system som sträcker sig från fysik till finansiering, är starkt partiska mot att producera enkla utgångar. Resultaten är förvånande, som naivt finns det ingen anledning att misstänka att en utgång borde vara mer sannolik än någon annan.
Forskarna, Kamaludin Dingle, Chico Q. Camargo, och Ard A. Louis, vid University of Oxford och vid Gulf University for Science and Technology, har publicerat en uppsats om sina resultat i ett nyligen utgåva av Naturkommunikation .
"Den största betydelsen av vårt arbete är vår förutsägelse att enkelhetsfördomar - att enkla utgångar är exponentiellt mer benägna att genereras än komplexa utgångar - gäller för en mängd olika system inom vetenskap och teknik, "Berättade Louis Phys.org . "Enkelhetens partiskhet innebär att, för ett system som består av många olika samverkande delar - säg, en krets med många komponenter, ett nätverk med många kemiska reaktioner, etc. - de flesta kombinationer av parametrar och ingångar bör resultera i enkelt beteende. "
Arbetet drar från området algoritmisk informationsteori (AIT), som behandlar sambandet mellan datavetenskap och informationsteori. Ett viktigt resultat av AIT är kodningssatsen. Enligt denna sats, när en universell Turing -maskin (en abstrakt beräkningsenhet som kan beräkna vilken funktion som helst) ges en slumpmässig ingång, enkla utdata har en exponentiellt högre sannolikhet att genereras än komplexa utdata. Som forskarna förklarar, detta resultat står helt i strid med den naiva förväntan att alla resultat är lika troliga.
Trots dessa spännande fynd, hittills har kodningssatsen sällan tillämpats på några verkliga system. Detta beror på att satsen bara har formulerats på ett mycket abstrakt sätt, och en av dess nyckelkomponenter - ett komplexitetsmått som kallas Kolmogorov -komplexiteten - är okompatibelt.
"Kodningssatsen för Solomonoff och Levin är ett anmärkningsvärt resultat som verkligen borde vara mycket mer allmänt känt, "Sa Louis." Det förutspår att utgångar med låg komplexitet är exponentiellt mer benägna att genereras av en universell Turing-maskin (UTM) än utgångar med hög komplexitet. Eftersom allt som kan beräknas kan beräknas på en UTM, det är en ganska fantastisk förutsägelse!
"Dock, kodningssatsen har förblivit oklar eftersom UTM är ganska abstrakt, eftersom det bara kan bevisas hålla i den asymptotiska gränsen för stora komplexiteter, och eftersom Kolmogorov -måttet som används för att bestämma komplexitet är i grunden okomputerat. Vårt arbete kringgår dessa problem med en något svagare version av kodningssatsen som är mycket lättare att tillämpa. "
I det nya, svagare version av kodningssatsen, forskarna ersatte Kolmogorov -komplexiteten med en approximationskomplexitet, som kan beräknas, samtidigt som den exponentiella preferensen för enkelhet bevaras. Den svagare kodningssatsen kan enkelt tillämpas för att göra förutsägelser om praktiska system.
"Vi använder språket för input-output-kartor, som kanske låter ganska abstrakt, "Sa Louis." Men många studerade system inom vetenskap och teknik omvandlar någon form av input till någon form av output via en algoritm. Till exempel, informationen som är kodad i DNA från en organism (dess genotyp) kan ses som input, medan organismens egenskaper och beteende (dess fenotyp) kan ses som produktionen. I en uppsättning differentialekvationer, ingången är parametrarna för ekvationerna, och utgången är lösningen på dessa ekvationer, med vissa gränsvillkor.
"Vi hävdar att om du slumpmässigt valde inmatningsparametrar, då är sådana system exponentiellt mer benägna att producera enkla utdata över komplexa utgångar. Eftersom denna förutsägelse gäller för ett brett utbud av kartor, vi gör ett brett påstående. Men det är en av dess styrkor. Vår härledning kräver inte att man vet så mycket om hur kartan (eller algoritmen) i fråga faktiskt fungerar.
"Så den viktigaste betydelsen av vårt arbete är att vår svagare version av kodningssatsen ungefär bibehåller den exponentiella förspänningen mot enkelheten i det ursprungliga kodningssatsen, men är mycket lättare att applicera i praktiken. "
En konsekvens av resultaten är att det är möjligt att förutsäga sannolikheten för ett visst resultat utifrån dess komplexitet. Även om en enkel utmatning är exponentiellt mer sannolikt att visas än en komplex utgång, forskarna noterar att detta inte nödvändigtvis betyder att enkla utgångar är mer benägna att visas än komplexa utgångar i allmänhet, eftersom det kan finnas många mer komplexa utgångar än enkla totalt sett.
För att illustrera några applikationer, forskarna använde den modifierade kodningssatsen för att analysera system av RNA -sekvenser, dygnsrytmer, och finansmarknaderna, och visade att alla dessa system uppvisar enkelhetsförspänningen. I framtiden, de planerar också att tillämpa resultaten på datoralgoritmer, biologisk utveckling, och kaotiska system. Dock, för en mer intuitiv förklaring av vad enkelhet fördom betyder, forskarna beskriver ett scenario som involverar våra primat släktingar:
"Tänk på det välkända problemet med apor som skriver på en skrivmaskin, "Sa Louis." Om aporna skriver på ett verkligt slumpmässigt sätt, och skrivmaskinen har N nycklar, då sannolikheten att få en viss längdsekvens k är bara 1/ N k , eftersom det finns en 1/ N chans att få rätt tangenttryckning vid var och en av k steg. Alltså varje sekvens av längd k är lika troligt eller osannolikt.
"Tänk nu på fallet där aporna skriver in i ett datorprogram. De kan då av misstag skriva ett kort program som genererar en lång utmatning. Till exempel, det finns en kod på 133 tecken i programmeringsspråket C som korrekt genererar de första 15, 000 siffror π. Så istället för 1/ N 15, 000 , vilken är sannolikheten för att apor får det här rätt på en skrivmaskin, oddsen är mycket lägre, endast 1/ N 133 , att aporna genererar π på datorn.
Det visar sig att de flesta siffror inte har korta program som genererar dem, så det bästa aporna på datorn kan göra för dessa nummer är att skriva ut ett program som 'utskriftsnummer, 'vilket är nära sannolikheten för att de skulle få det rätt på en skrivmaskin i alla fall. Men för enkla utgångar, sannolikheten är mycket högre än för skrivmaskinen. Per definition, enkla utdata definieras som de som har korta program som beskriver dem, och komplexa utdata är de som bara kan beskrivas med långa program. Så π är, per definition, ett nummer med låg komplexitet, och därför är det mycket mer sannolikt att det genereras av apor som skriver in i ett datorprogram än många andra nummer som inte är enkla.
"Vad kodningssatsen gör är att göra denna intuitiva berättelse kvantitativ. Korta program skrivs mer sannolikt slumpmässigt, och eftersom sannolikheter för längd k program också skala som 1/ N k , enkla utdata är exponentiellt mycket mer benägna att visas än komplexa. Vårt bidrag är att visa hur man enkelt beräknar det exponentiella sambandet mellan sannolikhet och komplexitet för många praktiska system. Vad som är trevligt är att du inte behöver veta mycket om kartan (eller motsvarande algoritmen) för att räkna ut om en utgång sannolikt kommer att visas eller inte. Till en bra första approximation, ju mer komprimerbar en utgång är, desto mer sannolikt är det att det visas vid slumpmässiga inmatningar. "
© 2018 Phys.org