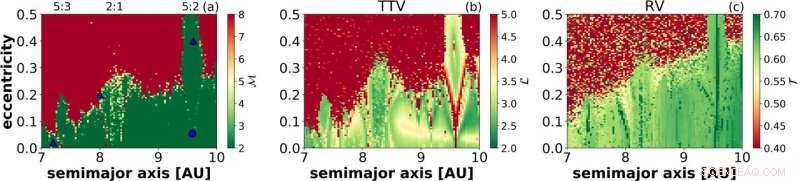
En stabilitetskarta över Saturnus erhållen genom kaosindikator MEGNO (a) och återkommande nätverk mäter genomsnittlig väglängd (b) och transitivitet (c). De två sistnämnda panelerna är baserade på transittidsvariation av Jupiter och solens radiella hastighet, respektive. Kredit:Tamás Kovács
Exoplaneter som kretsar kring avlägsna stjärnor kommer snabbt i fokus med avancerad teknik som rymdteleskopet Kepler. Det är svårt att få full förståelse för dessa system, eftersom exoplaneternas initiala positioner och hastigheter är okända. Att avgöra om systemdynamiken är kvasi-periodisk eller kaotisk är krångligt, dyrt och beräkningskrävande.
Under den här veckan Kaos , Tamás Kovács levererar en alternativ metod för stabilitetsanalys av exoplanetära kroppar som endast använder de observerade tidsseriedata för att härleda dynamiska mätningar och kvantifiera oförutsägbarheten hos exoplanetsystem.
"Om vi inte känner till de styrande ekvationerna för ett systems rörelse, och vi har bara tidsserierna - det vi mäter med teleskopet - då vill vi förvandla dessa tidsserier till ett komplext nätverk. I detta fall, det kallas ett återkommande nätverk, " Sa Kovács. "Detta nätverk innehåller alla de dynamiska egenskaperna hos det underliggande systemet vi vill analysera."
Papperet bygger på fysikern Floris Takens arbete, som föreslog 1981 att dynamiken i ett system skulle kunna rekonstrueras med hjälp av en serie observationer om systemets tillstånd. Med Takens inbäddningssats som utgångspunkt, Kovács använder inbäddning av tidsfördröjning för att rekonstruera en högdimensionell bana och sedan identifiera återkommande punkter, där kroppar i fasrummet ligger nära varandra.
"Dessa speciella punkter kommer att vara hörn och kanter av det komplexa nätverket, "Sa Kovács." När du väl har nätverket, du kan programmera om detta nätverk för att kunna tillämpa åtgärder som transitivitet, genomsnittlig sökvägslängd eller andra som är unika för det nätverket. "
Kovács testar metodens tillförlitlighet med ett känt system som modell, Saturnus trekroppssystem, Jupiter och solen, och applicerar den sedan på Kepler 36b och 36c -systemet. Resultaten från hans Kepler-system överensstämmer med vad som är känt.
"Tidigare studier påpekade att Kepler 36b och 36c är ett mycket speciellt system, eftersom från den direkta simuleringen och de numeriska integrationerna, vi ser att systemet är i utkanten av kaoset, " sa Kovács. "Ibland, den visar regelbunden dynamik, och vid andra tillfällen, det verkar vara kaotiskt."
Författaren planerar att sedan tillämpa sina metoder på system med mer än tre kroppar, testa dess skalbarhet och utforska dess förmåga att hantera längre tidsserier och skarpare datauppsättningar.