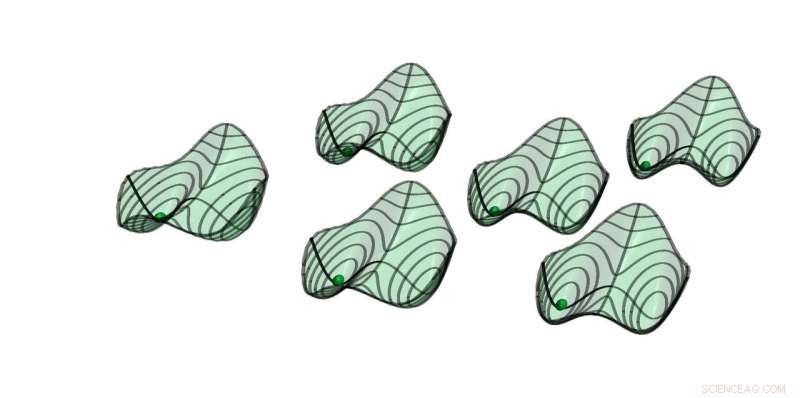
Kvasipotentialer för sex parametriska oscillatorer med svag allt-till-alla-koppling. Stabila lösningar finns vid minima. Bollarna indikerar den symmetriska lösningen, där alla oscillatorer är i fas. (Skärmdump från medföljande animering) Kredit:ETH Zurich/D-PHYS Toni Heugel
Strukturer som kallas tidskristaller, som i tid upprepar hur konventionella kristaller upprepas i rymden, har nyligen fångat forskarnas intresse och fantasi över discipliner. Begreppet har kommit fram ur sammanhanget för kvantmångkroppssystem, men ETH -fysiker har nu utvecklat en mångsidig ram som förtydligar kopplingar till klassiska verk från nästan två århundraden, vilket ger en enande plattform för att utforska till synes olikartade fenomen.
I en kristall, atomer är mycket ordnade, upptar väldefinierade platser som bildar rumsliga mönster. Sju år sedan, Nobelpristagaren i fysik 2004, Frank Wilczek, funderade över möjligheten till en tidsanalog av kristallin rumslig ordning-system som visar ihållande periodiska tidsmoduleringar i sitt lägsta energitillstånd. Konceptet med sådana strukturer med ett oscillerande marktillstånd är mycket spännande. Ack, inte långt efter att idén publicerades, det bevisades att sådana tidskristaller inte är möjliga utan att bryta fysikaliska grundlagar. Dock, efterföljande teoriorbete föreslog att när kvantmångkroppssystem periodiskt drivs, nya ihållande tidskorrelationer dyker upp som framkallar Wilczeks tidskristaller. Dessa drivna system kallades diskreta tidskristaller, och 2017, de första experimentella insikterna om sådana tillstånd rapporterades i ensembler av kopplade partiklar (joner, elektroner och kärnor) som visar kvantmekaniska egenskaper.
En inte så kort historia av tidskristaller
Inom kort, kloka observatörer såg tydliga likheter mellan diskreta tidskristaller i kvantsystem och så kallade parametriska resonatorer, ett begrepp i klassisk fysik som återvände till arbetet av Michael Faraday 1831. Kopplingen mellan dessa två arbetsformer förblev, dock, ogenomskinlig. Nu, teoretiker har utvecklat ett nytt ramverk som går långt för att lyfta oklarheterna kring likheterna mellan periodiskt drivna klassiska och kvantsystem.
Skriver i en artikel som publicerades idag i tidningen Fysiska granskningsbrev , Toni Heugel, en doktorsexamen student vid fysiska institutionen vid ETH Zürich, och Matthias Oscity, en student vid samma institution, arbetar med Dr. Ramasubramanian Chitra och professor Oded Zilberberg från Institute for Theoretical Physics och med Dr. Alexander Eichler från Laboratory for Solid State Physics, rapportera teoretiskt och experimentellt arbete som fastställer hur diskreta tidskristaller kan genereras som, å ena sidan, kräver inga kvantmekaniska effekter och, å andra sidan, visa äkta mångakroppseffekter, vilket är en egenskap hos diskreta tidskristaller som rapporteras i kvantsystem.
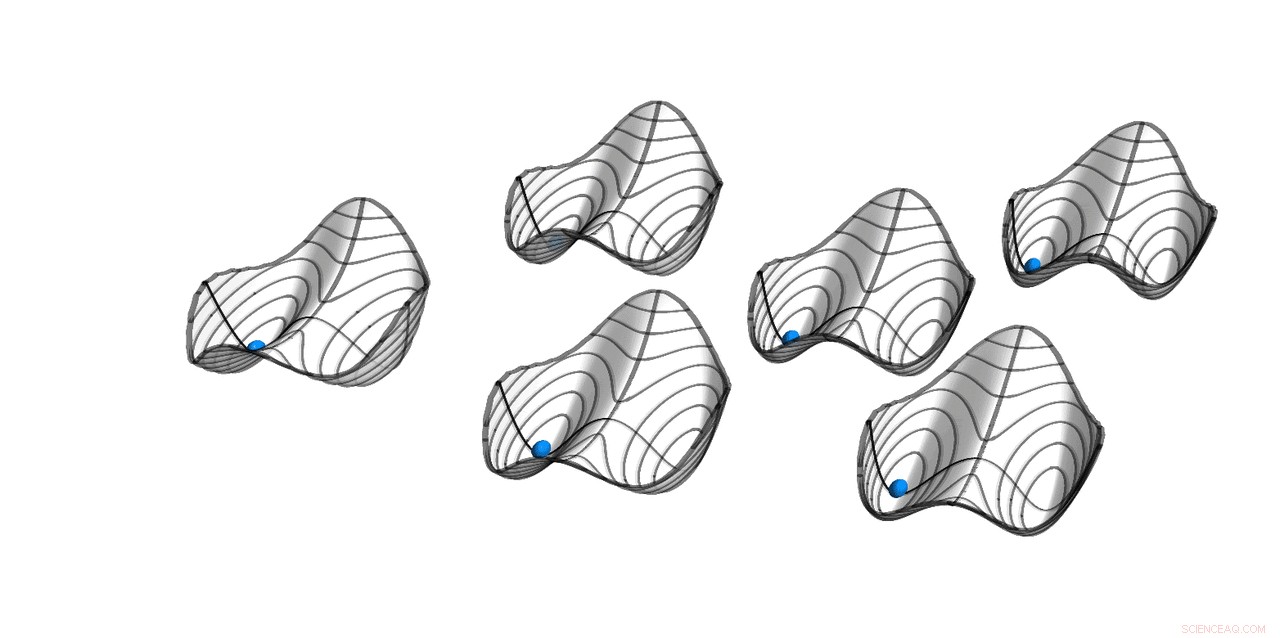
Kvasipotentialer för sex parametriska oscillatorer med svag allt-till-alla-koppling. Stabila lösningar finns vid minima. Bollarna indikerar den symmetriska lösningen, där alla oscillatorer är i fas. Hamiltonian H styr systemets rörelse med period T, medan själva lösningen har period 2T. Denna diskreta tidsöversättningssymmetribrytning gör systemet till en diskret tidskristall. Upphovsman:ETH Zurich/D-PHYS Toni Heugel
Många sätt att subharmoniska frekvenser
Det finns en uppenbar likhet mellan klassiska parametriska resonatorer och experimentellt realiserade diskreta tidskristaller i kvantmångkroppssystem:Båda visar framväxande dynamik vid frekvenser som är bråkdelar av drivfrekvensen. I samband med diskreta tidskristaller, framväxten av oscillationer vid sådana subharmoniska frekvenser bryter det drivna systemets tidsperiodicitet, tillhandahålla en 'tidsanalog' till kristallin rumslig ordning, där rymdens symmetri bryts. I klassiska parametriskt drivna system, subharmoniska frekvenser visas på mer bekanta sätt:Ett barn i en gunga, till exempel, modifierar tyngdpunkten vid dubbelt så hög frekvens som den resulterande oscillationen, eller hästsvansen hos en löpare oscillerar vid halva frekvensen av den vertikala huvudrörelsen.
Men har dessa olika fenomen något att göra med varandra? Ja, säger ETH -fysikerna. Särskilt, de anger var många kroppsaspekter förekommer i klassiska system. Att göra så, de övervägde klassiska olinjära oscillatorer med avstämbar koppling mellan dem.
Enande ram för periodiskt drivna klassiska och kvantsystem
Det är välkänt att för vissa körfrekvenser och styrkor, parametriska oscillatorer blir instabila och genomgår sedan en så kallad periodfördubbling, utöver vilket de svänger med halva körfrekvensen. Heugel, Oscity och deras kollegor utforskar vad som händer när flera sådana oscillatorer kopplas ihop. I beräkningar såväl som i experiment med två strängar med variabel koppling mellan dem, de hittar två distinkta regimer. När kopplingen är stark, systemet med två strängar rör sig kollektivt, återskapar i huvudsak barnets rörelser på en gunga eller en löpares hästsvans. Dock, vid svag koppling mellan strängarna, dynamiken för varje sträng liknar den som visas av det frikopplade systemet. Som en konsekvens, de kopplade oscillatorerna bifurkerar inte kollektivt utan bifurkerar individuellt vid lite olika parametrar för frekvensomriktaren, vilket leder till en rikare övergripande dynamik, som blir allt mer komplexa i takt med att systemen blir större.
ETH-forskarna hävdar att sådana svagt kopplade lägen liknar de som dyker upp i kvantmångkroppssystem, vilket innebär att deras ram kan förklara beteenden som ses experimentellt i dessa system. Dessutom, det nya verket föreskriver allmänna villkor för att generera klassiska kristaller med många kroppstider. Dessa kan i slutändan användas för att både tolka och utforska egenskaper hos deras kvantmotsvarigheter.
Tagen tillsammans, dessa fynd ger därför en kraftfull enande ram för periodiskt drivna klassiska och kvantsystem som visar dynamik vid framväxande subharmoniska frekvenser - system som hittills beskrivits i mycket olika sammanhang, men kanske inte alls så olik.