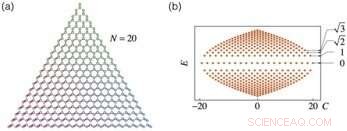
a. SL med platsvarierande kopplingsstyrkor. b. Energispektrum för FSL. Upphovsman:Science China Press
Sedan upptäckten av kvanthalleffekten, topologiska faser av elektroner har blivit ett stort forskningsområde inom den kondenserade materiens fysik. Många topologiska faser förutsägs i gitter med specifik teknik för elektronisk hoppning mellan gitterplatser. Tyvärr, avståndet mellan närliggande platser i naturliga gitter (kristaller) är i storleksordningen en miljarddels meter, vilket gör sådan ingenjörskonst extremt svår. Å andra sidan, de fotoniska kristallerna har en mycket större skala. Enhetscellerna för fotonkristaller för synligt ljus är flera tusen gånger större än elektronernas. Därför, det är inte förvånande att människor tar till fotoniska analoger av topologiska faser genom att gräva fram likheten mellan Maxwell- och Schrodinger-ekvationerna, och ett forskningsområde vid namn topologisk fotonik har blomstrat.
Dock, fotoner och elektroner är lika olika som hundar och katter. Fotoner är sociala till sin natur. De älskar att hålla ihop (det är därför vi har lasrar). Elektroner hatar varandra. De har sina egna territorier enligt Fermi-uteslutningsprincipen. Topologisk fotonik baserad på analogen mellan Maxwell- och Schrodinger-ekvationerna tillhör klassisk optik, d.v.s. en klassisk vågsimulering av den elektroniska bandtopologin. Det är naturligt att fråga sig om kvantiserat ljus bäddar in nya topologiska faser bortom tolkningen av klassisk optik. Nyligen, Han Cai och Da-Wei Wang från Zhejiang University avslöjade de topologiska faserna i gitter av kvantiserade ljustillstånd.
Ljusets energi kan bara existera i diskreta förpackningar, ett icke-negativt heltal plus hälften av hν, där h är Planck-konstanten och ν är ljusets frekvens. Heltalet är antalet fotoner i det tillståndet, som kallas Fock-staten, och den ena hälften bidrar med vakuumfluktuationerna. Denna diskreta ljusenergi är nyckeln till att förklara spektra för den svarta kroppens strålning (t.ex. i en ugn, högre temperatur flyttar spektrat till den blå sidan av en regnbågsremsa). Ljuskvantisering har också djupgående konsekvenser i atom-fotoninteraktioner. När det finns n fotoner i ljusfältet, sannolikheten för en exciterad atom att avge en annan foton är proportionell mot n+1 (kom ihåg att fotoner är sociala och de älskar att nya medlemmar går med). När ljuset är begränsat i ett hålrum, energin som emitteras av atomen kan återupptas, vilket resulterar i en oscillation av atomen mellan exciterat och grundtillstånd, och oscillationsfrekvensen är proportionell mot kvadratroten ur n+1. Ett spektrum av dessa diskreta värden på oscillationsfrekvenserna kan observeras när atomen är kopplad med ljus i en överlagring av Fock-tillstånd, d.v.s. i Jaynes-Cummings (JC)-modellen, som har blivit en standardmetod för att erhålla ljusets kvanttillstånd.
Det är inte uppenbart att JC-modellen är relaterad till topologiska faser, men denna kvadratrot-av-heltalsskalning av energispektrumet är en reminiscens av Landau-nivåerna av elektroner i en grafen, som är en vagga av topologiska faser. Energibanden av elektroner i en grafen berör två punkter på kanten av Brillouin-zonen, som heter Dirac-punkterna, där elektronerna som lyder den tvådimensionella Dirac-ekvationen har en linjär relation mellan dess energi och momentum. När ett magnetfält appliceras, elektronerna gör cyklotronrörelser med diskreta frekvenser som skalar med kvadratroten ur heltal, som motsvarar diskreta Landau-nivåer. Cai och Wang etablerade kopplingen mellan tre-mods JC-modellen och Dirac-elektronerna i ett magnetfält.
I en tre-mods JC-modell där en atom är kopplad till tre kavitetslägen, kvanttillstånden kan fullständigt beskrivas med fyra heltal (x, y, z, q), där x, y och z är fotontalen i de tre kavitetslägena, och q=0 och 1 för atomens grundtillstånd och exciterade tillstånd. I JC-modellen, alla (N+1)^2 tillstånd som uppfyller x+y+z+q=N bildar ett bikakegitter, liknar en grafen och vi kallar det Fock-state gittret. Eftersom den exciterade atomen kan avge en foton till ett av kavitetslägena, tillståndet (x, y, z, 1) är kopplad till tre angränsande stater, (x+1, y, z, 0), (x, y+1, z, 0) och (x, y, z+1, 0). Dock, kopplingsstyrkorna till de tre kavitetslägena är proportionella mot kvadratroten av deras fotontal. För varje tillstånd (x, y, z, 1) det finns en konkurrens mellan de tre kaviteterna för att erhålla fotonen som emitteras av atomen, och kaviteterna som innehåller fler fotoner har en fördel, vilket kan förstås som fotonernas majoritetsprincip. Detta motsvarar en grafen som utsätts för en påfrestning som modifierar hoppkoefficienterna för elektroner från en plats till dess tre grannar.
Det visar sig att när kopplingsstyrkan mellan den mest tätbefolkade kavitetsmoden och atomen är större än summan av de andra två moderna, de två Dirac-punkterna smälter samman och en bandlucka öppnas, som är en Lifshitz topologisk övergång mellan en semimetall och en bandisolator. I den semimetalliska fasen, variationen av kopplingsstyrkan är ekvivalent med ett töjningsfält som inducerar ett effektivt magnetfält och leder till kvantiserade Landau-nivåer, utifrån vilken författarna undersökte dalhallseffekten och byggde en Haldane-modell i tre-mods JC-modellen.
Författarna undersökte också de endimensionella Fock-state gittren med endast två kavitetslägen. De är inneboende Su-Schriefer-Heeger-modeller och värdtopologiska kanttillstånd. Modellen kan utökas ytterligare till högre än tre dimensioner för topologiska faser som inte är tillgängliga i verkliga gitter. De föreslagna topologiska faserna är redo att realiseras i supraledande kretsar och är lovande för tillämpningar inom kvantinformationsbehandling.