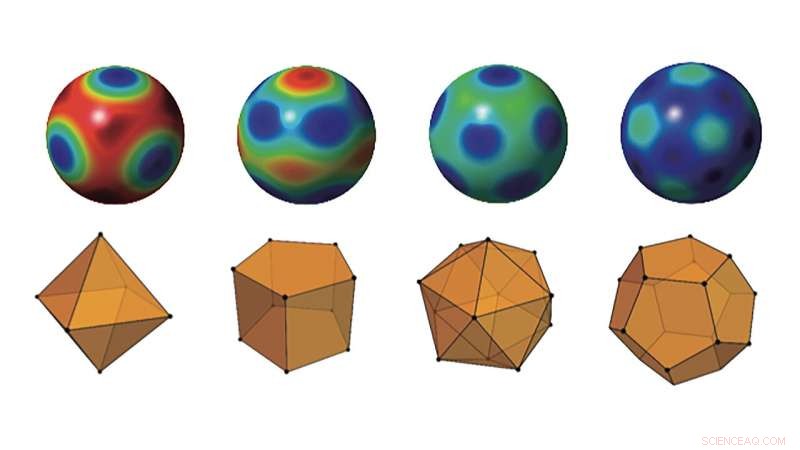
Majorana-konstellationer av några av de mest kvanttillstånd i olika dimensioner. Kredit:Luis L. Sánchez Soto
Stora föremål, som basebollar, fordon, och planeter, bete sig i enlighet med de klassiska mekanikens lagar formulerade av Sir Isaac Newton. Små, såsom atomer och subatomära partiklar, styrs av kvantmekanik, där ett föremål kan bete sig som både en våg och en partikel.
Gränsen mellan det klassiska och kvantvärlden har alltid varit av stort intresse. Forskning rapporterad i AVS Quantum Science , överväger frågan om vad som gör något "mer kvant" än ett annat - finns det något sätt att karakterisera "kvantitet"? Författarna rapporterar att de har hittat ett sätt att göra just det.
Graden av kvantitet är viktig för tillämpningar som kvantberäkning och kvantavkänning, som erbjuder fördelar som inte finns i deras klassiska motsvarigheter. För att förstå dessa fördelar krävs i tur och ordning, en förståelse för graden av kvantitet hos de inblandade fysiska systemen.
Istället för att föreslå en skala vars värden skulle associeras med graden av kvantitet, författarna till denna studie tittar på extrema, nämligen de tillstånd som antingen är mest kvant eller minst kvantum. Författaren Luis Sanchez-Soto sa att idén till studien kom från en fråga som ställdes vid ett vetenskapligt möte.
"Jag höll ett seminarium om detta ämne när någon ställde frågan till mig:" Ni inom kvantoptik pratar alltid om de mest klassiska tillstånden, men hur är det med de mest kvanttillstånden?'" sa han.
Man har länge förstått att så kallade koherenta tillstånd kan beskrivas som kvasiklassiska. Koherenta tillstånd uppstår, till exempel, i en laser, där ljus från flera fotonkällor är i fas vilket gör dem till det minsta kvantumet av tillstånd.
Ett kvantsystem kan ofta representeras matematiskt av punkter på en sfär. Denna typ av representation kallas en Majorana-konstellation, och för sammanhängande stater, konstellationen är helt enkelt en enda punkt. Eftersom dessa är det minsta antalet tillstånd, de mest kvanta skulle ha konstellationer som täcker mer av sfären.
Utredarna tittade på flera sätt som andra forskare har utforskat kvantitet och övervägde Majorana-konstellationen för varje sätt. De frågade sedan vad den mest jämnt fördelade uppsättningen poäng på en sfär för detta tillvägagångssätt är.
När Sanchez-Soto och hans kollegor övervägde frågan om kvantitet, de insåg att det var ett matematiskt projekt "av enorm skönhet, " förutom att vara användbar.