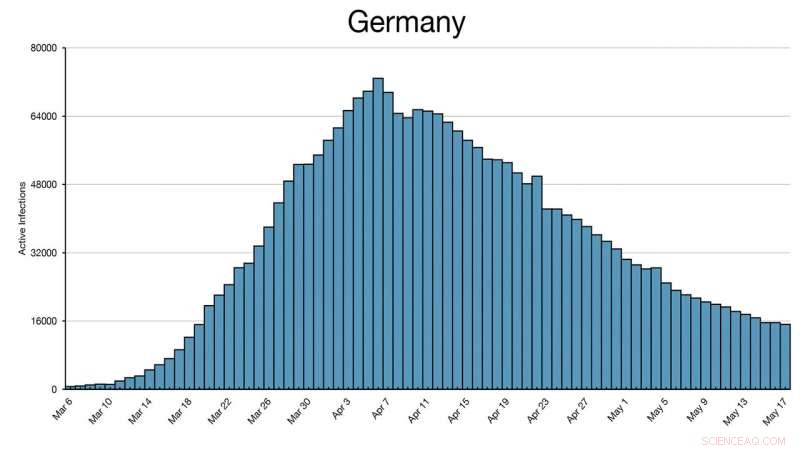
Detta histogram över Tyskland visar att det nådde sin topp den 4/6/20 och delvis öppnade igen i april. Gränsen mot Österrike förblev stängd förutom för arbetspendling. Gränserna öppnades igen 15/6/20, men masker bars i tyska företag in i juli. Tyskland förföll inte till nivån 3/16/20 förrän 6/10/20, nästan tre månader senare. Kredit:Joseph Lee McCauley
Under de första månaderna av covid-19-pandemin, Joseph Lee McCauley, en fysikprofessor vid University of Houston, tittade på de dagliga uppgifterna för sex länder och undrade om infektionerna verkligen växte exponentiellt. Genom att extrahera fördubblingstiderna från data, han blev övertygad om att de var det.
Fördubblingstid och exponentiell tillväxt går hand i hand, så det blev klart för honom att modellering baserat på tidigare infektioner är omöjligt, eftersom kursen förändras oförutsägbart från dag till dag på grund av social distansering och lockdown-ansträngningar. Och hastighetsförändringarna skiljer sig för varje land baserat på omfattningen av deras sociala distansering.
I AIP avancerar , McCauley förklarar hur han kombinerade matematik i form av Tchebychevs ojämlikhet med en statistisk ensemble för att förstå hur makroskopisk exponentiell tillväxt med olika dagliga hastigheter uppstår från person-till-person sjukdomsinfektion.
"Diskretiserade vanliga kemiska kinetiska ekvationer tillämpade på infekterade, oinfekterad, och återvunna delar av befolkningen tillät mig att organisera data, så att jag kunde separera effekterna av social distansering och återhämtning inom dagliga infektionsfrekvenser, " sa McCauley.
Platåing utan topp uppstår om återhämtningsgraden är för låg, och USA, STORBRITANNIEN., och Sverige faller i den kategorin. Ekvationer kan inte itereras för att se in i framtiden, eftersom morgondagens kurs är okänd tills den utvecklas.
"Modellerare tenderar att felaktigt tillämpa de kemiska kinetiska ekvationerna som SIR (känslig, Infektiös, eller återvunnen) eller SEIR (mottaglig, Utsatt, Infektiös, eller återställda) modeller, eftersom de försöker generera framtida kurser från tidigare kurser, "Sa McCauley. "Men det förflutna tillåter dig inte att använda ekvationer för att förutsäga framtiden i en pandemi, eftersom social distansering ändrar priserna dagligen."
McCauley upptäckte att han kunde göra en prognos inom fem sekunder via handräknare som är lika bra som vilken datormodell som helst genom att helt enkelt använda infektionsfrekvensen för idag och igår.
"Låsningar och socialt distansarbete, sade McCauley. "Jämför Österrike, Tyskland, Taiwan, Danmark, Finland, och flera andra länder som nådde sin topp i början av april, med USA, STORBRITANNIEN., Sverige, och andra utan lockdown eller halvhjärtade lockdowns – de har aldrig ens platåerat, mycket mindre toppade."
Han betonar att prognoser inte kan förutse toppar eller ens platåer. Platåing innebär inte toppar, och om toppar inträffar, det finns inget i data som visar när det kommer att hända. Det händer när återhämtningsgraden är högre än antalet nya infektioner.
"Social distansering och låsningar minskar infektionsfrekvensen men kan inte orsaka toppar, "Sade McCauley. "Social distansering och återhämtning är två separata termer inom de dagliga kinetiska hastighetsekvationerna."
Innebörden av detta arbete är att forskningspengar skulle kunna användas bättre än på dyr epidemimodellering.
"Politiker borde kunna tillräckligt med aritmetik för att få instruktioner om konsekvenserna, ", sa McCauley. "Effekten av låsningar och social distansering visar sig i de observerade fördubblingstiderna, och det finns också en förutspådd fördubblingstid baserat på två dagar, som fungerar som en bra framtidsprognos."