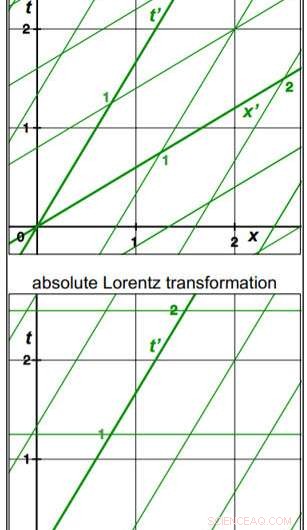
En av de mest grundläggande strukturella aspekterna av relativistisk rymdtid är beskrivningen av hur tid och avstånd förändras genom rörelse. Teorin om särskild relativitetsteori beskriver en rymdtidskonstruktion för linjär konstant rörelse där tid vidgas och längder dras ihop som svar på rörelse. Detta ramverk beskrivs av Lorentz -transformationen, som omfattar matematiska formler som beskriver hur tid och avstånd förändras mellan rörliga referensramar. Lorentz -transformationen beskriver också hur en stationär observatör ser på tiden i den rörliga ramen för att kompenseras med avstånd. Förskjutning av tid med avstånd mellan referensramar genererar differentiell samtidighet, där händelser som är samtidiga för en observatör inte kommer att vara samtidiga för en andra observatör som rör sig relativt den första observatören.

Typen av rymdtid i roterande ramar har inte fastställts på den mest grundläggande nivån för att definiera den transformation som exakt beskriver de relativistiska effekterna och samtidighetsramen. Det finns fyra distinkta rotationsrelativistiska transformationer i litteraturen:metoden Langevin; Eftertransformation; Franklin -transformation; och den absoluta Lorentz -transformationen (ALT) i sin rotationsform. Att bestämma vilken transformation som exakt beskriver experimentella data skulle indikera rymdtidens ramverk som finns i verkliga roterande ramar. Att förstå denna grundläggande information har stor tillämpbarhet eftersom majoriteten av synlig materia i universum är i rotationsrörelse, inklusive den roterande jorden.

Den mest citerade rotationsomvandlingen är metoden Langevin, som först beskrevs 1921. Under årtiondena har metoden Langevin har använts för att beskriva relativitet i roterande ramar i hundratals läroböcker och forskningsartiklar. Dock, metoden Langevin har aldrig bedömts med experimentella data som har tillräcklig upplösning för att skilja den från de andra stora rotationsomvandlingarna.

En transformations kombination av relativistiska effekter och samtidighetsramverk påverkar hur ljuset förökar sig. De fyra transformationerna har olika förutsägelser för den envägs ljushastigheten i roterande ram, tvåvägs ljushastighet, och Sagnac -effekten. Denna studie härleder de optiska förutsägelserna för varje transformation direkt från deras transformationsekvationer, med flera av de förutsägelser som inte tidigare rapporterats i litteraturen. Prognoserna jämförs sedan med senaste högupplösta optiska experimentella data.

Optisk resonatordata om ljusets tvåvägshastighet är bland de högsta upplösta vetenskapliga mätningarna, med resolutioner av 10 ^-18 . Denna höga upplösning krävs för att skilja mellan transformationernas förutsägelser. Studien avslöjar att ALT och Franklin-transformationen förutsäger den konstanta tvåvägs ljushastigheten, c, matchar data för optisk resonator, medan Langevin -metriska och Post -transformationsprognoser ogiltigförklaras av data. Misslyckandet med Langevin -metriken och Post -transformationen för att matcha optisk resonatordata visas att bero på att de inte uppvisar någon (eller ingen netto) längdkontraktion i den roterande ramen. I kontrast, ALT- och Franklin -transformationerna uppvisar längdkontraktion, vilket möjliggör deras exakta förutsägelser för ljusets tvåvägshastighet.

Data om Sagnac -effekten, som har lägre upplösningar på 10 ^-8 , är kompatibel med Sagnac -effektprognoserna för Langevin -mätvärdet, Posta, och ALT -transformationer, men är oförenlig med Franklin -transformationen, som förutspår ingen Sagnac -effekt. Franklin -transformationens misslyckande med att generera en uppenbar Sagnac -effekt visar sig bero på dess införlivande av differentiell samtidighet. I kontrast, de andra tre transformationerna innehåller absolut samtidighet där tiden inte förskjuts med avstånd, vilket tillåter uppenbara Sagnac -effekter. Således, ALT är den enda transformationen som exakt beskriver hela spektret av relativistiska optiska data.

Flera publikationer har föreslagit mekanismer för att införliva differentiell samtidighet i roterande ramar för att möjliggöra generering av en uppenbar Sagnac -effekt. Dock, dessa mekanismer genererar alternativa Sagnac -effektekvationer. Studien visar att dessa alternativa Sagnac-effektekvationer innebär tvåvägs ljushastigheter som ogiltigförklaras av högupplösta optiska resonatordata. I kontrast, ALT förutspår den konventionella Sagnac -effekten, vilket innebär den konstanta tvåvägs ljusets hastighet, c.

Studien visar att rotationsomvandlingen ALT exakt förutsäger både högupplösta optiska data och icke-optiska relativistiska observationer med roterande ram. Denna analys innebär att ALT -rotationsomvandlingen beskriver den grundläggande ramen för rymdtid i roterande ramar. Detta förtydligar att rymdtid med roterande ram kännetecknas av de relativistiska effekterna av tidsutvidgning och längdkontraktion inom ett absolut samtidighetsramverk där tid inte kompenseras med avstånd.