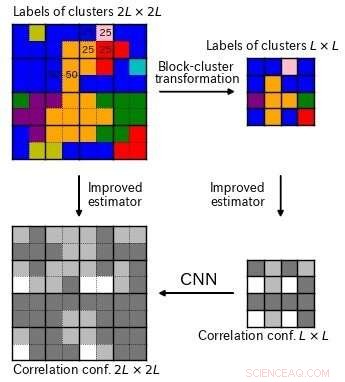
En korrelationskonfiguration (överst till vänster) reduceras med en nyutvecklad blockklustertransformation (överst till höger). Både den ursprungliga och reducerade konfigurationen har en förbättrad estimatorteknik tillämpad för att ge konfigurationspar av olika storlek (nedre raden). Med hjälp av dessa träningspar, en CNN kan lära sig att konvertera små mönster till stora, uppnå en framgångsrik omvänd RG -transformation. Upphovsman:Tokyo Metropolitan University
Forskare från Tokyo Metropolitan University har förbättrat "superupplösta" maskininlärningstekniker för att studera fasövergångar. De identifierade nyckelfunktioner för hur stora arrayer av interagerande partiklar beter sig vid olika temperaturer genom att simulera små arrayer innan de använde ett konvolutionellt neuralt nätverk för att generera en bra uppskattning av hur en större array skulle se ut med hjälp av korrelationskonfigurationer. Den enorma besparingen i beräkningskostnaderna kan innebära unika sätt att förstå hur material beter sig.
Vi är omgivna av olika tillstånd eller faser av materia, dvs gaser, vätskor, och fasta ämnen. Studiet av fasövergångar, hur en fas förvandlas till en annan, ligger i hjärtat av vår förståelse av materia i universum, och förblir ett hett ämne för fysiker. Särskilt, tanken på universalitet, där väldigt olika material beter sig på liknande sätt tack vare några delade funktioner, är en kraftfull sådan. Det är därför fysiker studerar modellsystem, ofta enkla rutnät av partiklar på en array som interagerar via enkla regler. Dessa modeller destillerar essensen av den gemensamma fysiken som delas av material och, otroligt, fortfarande uppvisar många av egenskaperna hos verkliga material, som fasövergångar. På grund av deras eleganta enkelhet, dessa regler kan kodas in i simuleringar som berättar hur material ser ut under olika förhållanden.
Dock, som alla simuleringar, besväret börjar när vi vill titta på många partiklar samtidigt. Beräkningstiden som krävs blir särskilt oöverkomliga nära fasövergångar, där dynamiken saktar ner, och korrelationens längd, ett mått på hur tillståndet för en atom förhåller sig till tillståndet för en annan ett stycke bort, växer sig större och större. Detta är ett verkligt dilemma om vi vill tillämpa dessa fynd på den verkliga världen:verkliga material innehåller i allmänhet alltid många fler storleksordningar för atomer och molekyler än simulerad materia.
Det är därför ett team ledd av professorerna Yutaka Okabe och Hiroyuki Mori från Tokyo Metropolitan University, i samarbete med forskare vid Shibaura Institute of Technology och Bioinformatics Institute of Singapore, har studerat hur man på ett tillförlitligt sätt extrapolerar mindre simuleringar till större med hjälp av ett koncept som kallas en omvänd renormaliseringsgrupp (RG). Renormaliseringsgruppen är ett grundläggande begrepp i förståelsen av fasövergångar och ledde till att Wilson fick Nobelpriset i fysik 1982. Nyligen, fältet träffade en kraftfull allierad i konvolutionella neurala nätverk (CNN), samma verktyg för maskininlärning som hjälper datorsyn att identifiera objekt och dechiffrera handstil. Tanken skulle vara att ge en algoritm tillståndet för en liten uppsättning partiklar och få den att uppskatta hur en större uppsättning skulle se ut. Det finns en stark analogi med tanken på superupplösta bilder, där blockig, pixlade bilder används för att generera jämnare bilder med högre upplösning.
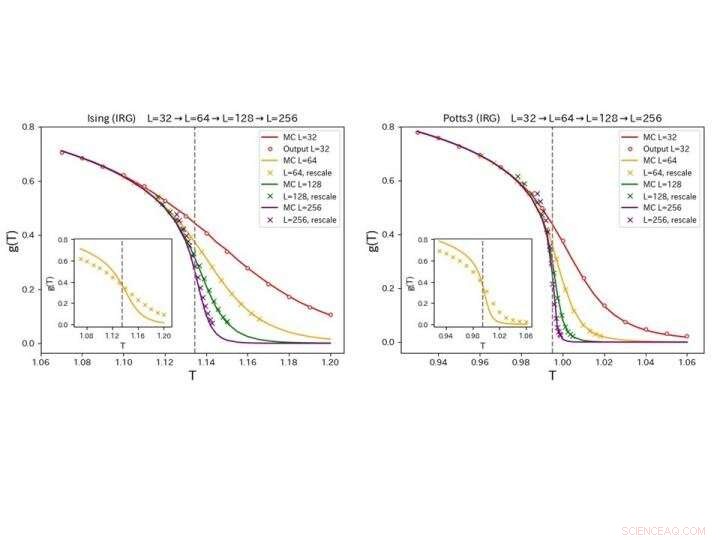
Trender som hittats från simuleringar av större system återges troget av de tränade CNN:erna för både Ising (vänster) och tre-stats Potts (höger) modeller. (infälld) Korrekt temperaturskalning uppnås med data med någon godtycklig systemstorlek. Upphovsman:Tokyo Metropolitan University
Teamet har tittat på hur detta tillämpas på spinnmodeller av materia, där partiklar interagerar med andra närliggande partiklar via riktningen för deras snurr. Tidigare försök har särskilt kämpat för att tillämpa detta på system vid temperaturer över en fasövergång, där konfigurationer tenderar att se mer slumpmässiga ut. Nu, istället för att använda snurrkonfigurationer, dvs. enkla ögonblicksbilder i vilken riktning partikelspinnarna pekar, de övervägde korrelationskonfigurationer, där varje partikel kännetecknas av hur likt dess eget spinn är det hos andra partiklar, speciellt de som är väldigt långt borta. Det visar sig att korrelationskonfigurationer innehåller mer subtila köer om hur partiklar är ordnade, särskilt vid högre temperaturer.
Liksom alla maskininlärningstekniker, nyckeln är att kunna generera en pålitlig träningsuppsättning. Teamet utvecklade en ny algoritm som kallas block-cluster transformation för korrelationskonfigurationer för att minska dessa till mindre mönster. Att tillämpa en förbättrad estimatorteknik på både de ursprungliga och reducerade mönstren, de hade par av konfigurationer av olika storlek baserat på samma information. Allt som återstår är att träna CNN att konvertera de små mönstren till större.
Gruppen övervägde två system, 2D Ising-modellen och Potts-modellen med tre tillstånd, båda viktiga riktmärken för studier av kondenserat material. För båda, de fann att deras CNN kunde använda en simulering av ett mycket litet antal punkter för att återge hur ett mått på korrelationen g (T) förändrades över en fasövergångspunkt i mycket större system. Jämförelse med direkta simuleringar av större system, samma trender återges för båda systemen, kombinerat med en enkel temperaturomskalning baserad på data vid en godtycklig systemstorlek.
En framgångsrik implementering av omvända RG-transformationer lovar att ge forskare en glimt av tidigare otillgängliga systemstorlekar, och hjälpa fysiker att förstå material i större skala. Teamet hoppas nu kunna tillämpa sin metod på andra modeller som kan kartlägga mer komplexa funktioner som ett kontinuerligt utbud av snurr, samt studiet av kvantsystem.