Matematiska modeller har använts i stor utsträckning för att vägleda regeringsbeslut om covid-19-pandemin, från att prognostisera resultat till att till och med testa potentiella interventioner.

Dock, komplexiteten i verkliga scenarier ställer fortfarande nya teoretiska utmaningar för matematisk modellering av epidemispridning.

Till exempel, bevis från covid-19 superspridande händelser indikerar att det är svårt att definiera egenskaper hos dessa händelser, som kan variera avsevärt i varaktighet och antal personer som är inblandade.

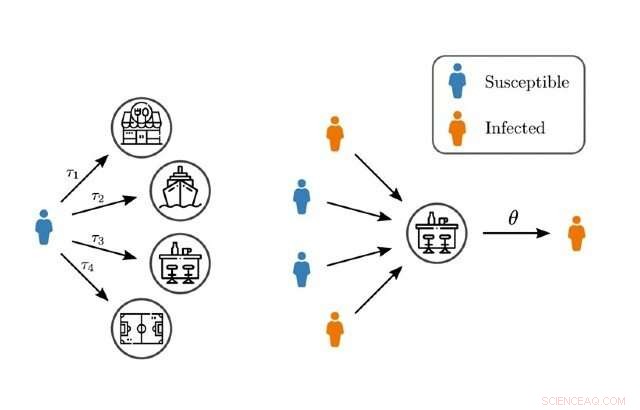
Befintliga nätverksmodeller för spridning av epidemier fokuserar ofta på kontakter mellan par av individer medan samlokalisering av individer som på arbetsplatsen, restauranger, eller gym inkluderar vanligtvis fler än två personer. De misslyckas också ofta med att beakta den heterogena tidsmässiga varaktigheten av dessa interaktioner på en specifik plats.

I en ny studie, publiceras idag i Fysiska granskningsbrev , forskare utvecklade en ny metod för epidemimodellering som tar hänsyn till interaktioner mellan två eller flera personer på samma plats och under olika lång tid.

Utmanande antaganden

Modellen utvecklad av det internationella forskarteamet, inklusive fysiker från University of Vermont och Université Laval, och leds av professor Ginestra Bianconi, en matematiker från Queen Mary University of London, tog även hänsyn till nya bevis som tyder på att en minimal infektionsdos krävs för att en infektion ska uppstå.

Denna nya modelleringsmetod förändrar radikalt väletablerade antaganden inom modellering av epidemiska nätverk, som infektionsfrekvenser som är linjära med antalet infekterade individer. Fynden visar att samlokaliseringar i kombination med heterogen exponeringstid kan leda till icke-linjära infektionsfrekvenser om en minimal infektionsdos är nödvändig för att en infektion sannolikt ska inträffa.

Professor Ginestra Bianconi, Professor i tillämpad matematik vid Queen Mary, sa:"Samlokalisering kan involvera grupper av människor, medan typiskt nätverksmodeller för epidemispridning är baserade på kontaktnätverk som beskriver parvisa interaktioner som kan ha en helt annan topologi än samlokaliseringskontaktnätverk. Samlokalisering sker också i tid, till exempel kan jag gå till samma gym som en annan person, men vi kanske inte alltid träffas och vi kanske tränar olika lång tid där."

"Vårt tillvägagångssätt omfattar heterogeniteter av interaktioner på grund av samlokalisering som sker mellan mer än två personer under olika lång tid och avslöjar att infektionskärnor kan vara icke-linjära i dessa mycket heterogena scenarier, vilket innebär att om det finns dubbelt så många infekterade individer som besöker en viss plats kan sannolikheten för infektion också vara mer än dubbelt så stor. Dessa resultat kastar nytt ljus över den mycket heterogena karaktären hos superspridande händelser i samband med COVID-19."