Ett par forskare från Universit´e Paris-Saclay, CNRS och Univ Rennes, CNRS, IPR, respektive, har använt matematik för att hjälpa till att beskriva processen när korta fibertrådar tvinnas till långa sträckor av garn. I deras artikel publicerad i tidskriften Physical Review Letters, Antoine Seguin och Jérôme Crassous beskriver hur de använde experiment och simuleringar för att bättre förstå de faktorer som är involverade när fibrer vrids ihop.

Människor har tvinnat samman korta trådar av fibrer för att skapa långa trådar av rep eller garn i tusentals år, och även om den övergripande processen är väl förstått, har matematiken bakom den varit ganska skissartad. I denna nya ansträngning har Seguin och Crassous tagit itu med problemet med ett nytt tillvägagångssätt och tillämpat både experiment och simuleringar.

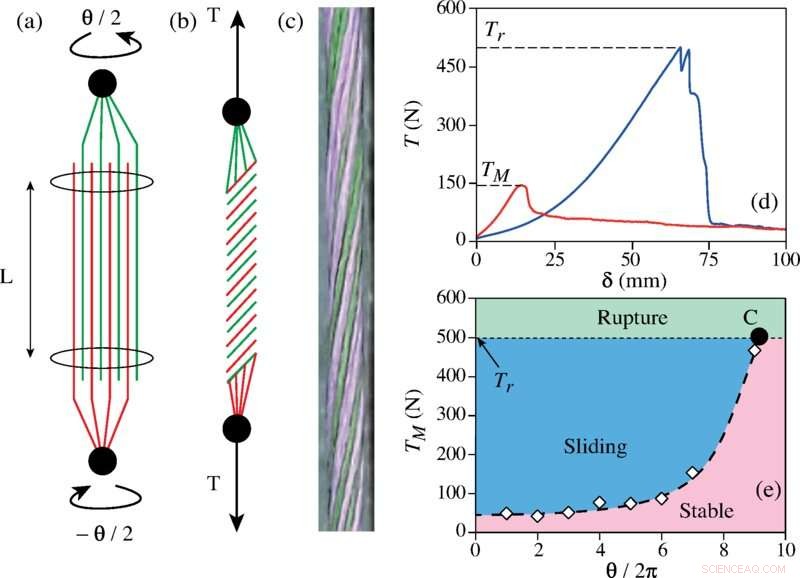
Eftersom flera korta fibrer tvinnas ihop blir de sammanflätade, men det räcker såklart inte för att hålla ihop dem. De håller ihop på grund av friktionen. Att dra i ändarna av en längd av garn tvingar de enskilda trådarna den är gjord av att trycka in i varandra, vilket ökar mängden friktion och därmed dess styrka. Men finns det matematiska regler som styr processen? Vilket är det optimala antalet fibrer, till exempel, för att säkerställa det starkaste garnet? Eller vilken grad av hållfasthet ges till garnet av graden av friktion mellan två fibersträngar?

För att hitta dessa svar genomförde forskarna flera tester på olika fibrer tvinnade till garn. De fann att en ökning av vridningar ökade fiberbindningsstyrkan - men bara upp till en viss punkt. Dessutom hade varje typ av fiber sin egen brytpunkt. När de skapade simuleringar för att enklare testa olika konfigurationer fann de också att det fanns en optimal fiberradie för en given längd av garn och att garnstyrkan skalas med exponentialen för kvadraten på tvinningsvinkeln.

När de letade efter gemensamma drag upptäckte de vad de beskriver som Hercules twist number - en parameter som beskriver krafterna involverade i vridningsvinkeln, en friktionskoefficient och garnets radie. De fann också att detta tal i allmänhet var proportionellt mot kvadraten på antalet vridningar som applicerades och hade ett kritiskt värde på 30. De utvecklade också en formel för att visa den optimala radiestorleken för en given typ av fiber. + Utforska vidare

Forskare undersöker "varför kläder inte faller isär"

© 2022 Science X Network